Rozwiązanie
Szkicujemy okręgi \(x^{2}+y^{2}=1\) oraz \((x-1)^{2}+(y-1)^{2}=1\) w układzie współrzędnych.
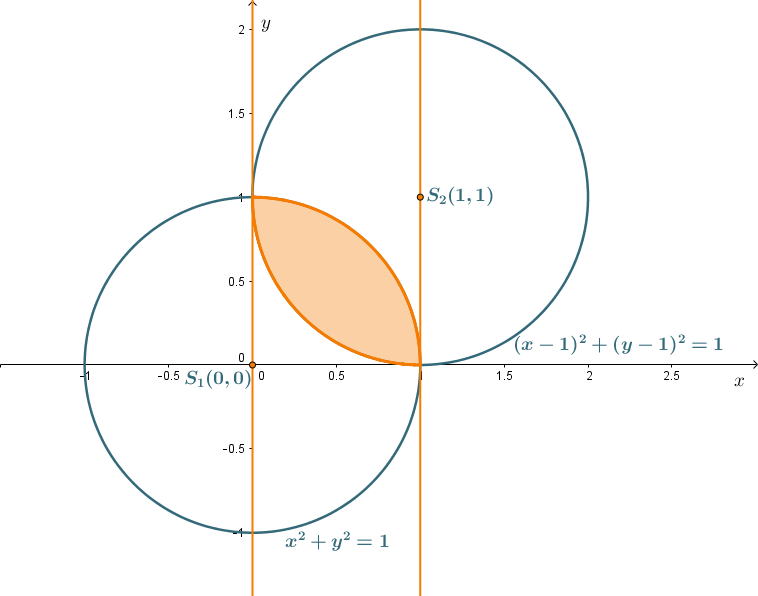
Pole zacieniowanego obszaru to całka oznaczona w granicach całkowania od \(0\) do \(1\) z różnicy funkcji opisującej krzywą \(x^{2}+y^{2}=1\) w pierwszej ćwiartce układu współrzędnych oraz krzywą \((x-1)^{2}+(y-1)^{2}=1\) (dolna część) .
Wyznaczamy z równań okręgów \(y.\)
\(x^{2}+y^{2}=1\\
y^{2}=1-x^{2}\\
y=\pm \sqrt{1-x^{2}}\)
Wybieramy dodatni znak, gdyż interesuje nas część okręgu znajdująca się nad osią \(Ox.\)
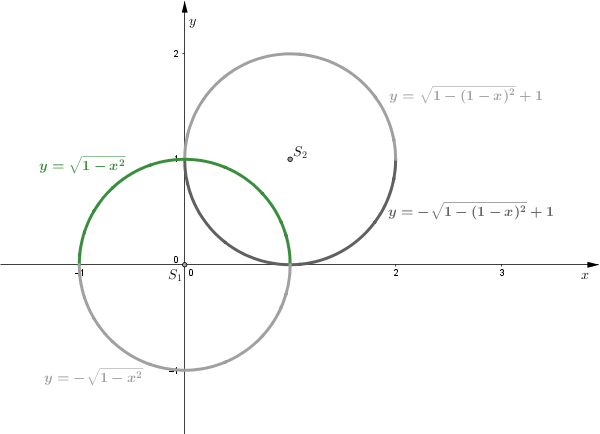
\((x-1)^{2}+(y-1)^{2}=1\\
(y-1)^{2}=1-(x-1)^{2}\\
y-1=\pm \sqrt{1-(x-1)^{2}}\)
Wybieramy ujemny znak pierwiastka, gdyż (przed przesunięciem o 1 jednostkę w górę) interesuje nas ta część okręgu, która znajduje się pod osią \(Ox.\)
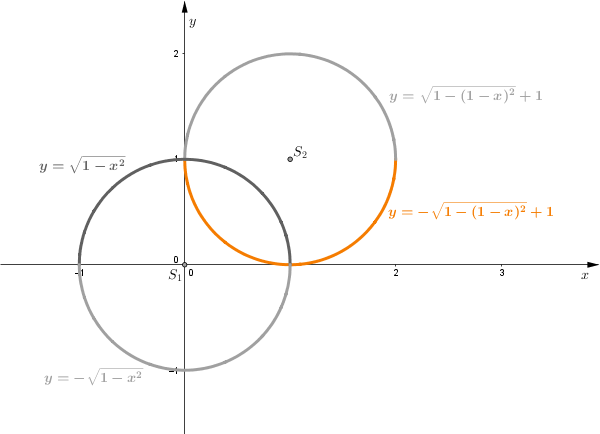
Zatem pole zacieniowanego obszaru wynosi:
\[{\displaystyle |P|=\int_{0}^{1}\left [\sqrt{1-x^{2}}-\left (\sqrt{1-(x-1)^{2}}+1 \right ) \right ]\ dx=\int_{0}^{1}\left [\sqrt{1-x^{2}}+\sqrt{1-(x-1)^{2}}-1 \right ]\ dx=\int_{0}^{1}\sqrt{1-x^{2}}\ dx+\int_{0}^{1} \sqrt{1-(x-1)^{2}}\ dx- \int_{0}^{1} 1\ dx =\cdots }\]
Dla wygody dzielimy całkę na trzy oddzielne i liczymy osobno, aby wrócić do liczenia pola powierzchni obszaru, tj.
\({\displaystyle =\int_{0}^{1}\frac{1-x^{2}}{\sqrt{1-x^{2}}}\ dx=\int_{0}^{1}\frac{dx}{\sqrt{1-x^{2}}}-\int_{0}^{1}\frac{x^{2}}{\sqrt{1-x^{2}}}\ dx=\begin{vmatrix}
x=\sin t\\
dx=\cos t\ dt
\end{vmatrix}=\Big[ \textrm{arcsin }x \Big ]_{0}^{1}-\int_{0}^{\frac{\pi}{2}\color{#F57C00}{(^{*})}}\frac{\sin^{2}t\cos t\ dt}{\sqrt{1-\sin^{2}t}}=\Big[ \textrm{arcsin }1-\textrm{arcsin }0 \Big ]-\int_{0}^{\frac{\pi}{2}}\frac{\sin^{2}t \cos t\ dt}{\cos t \color{#F57C00}{(^{**})}}=\Big[ \textrm{arcsin }1-0 \Big ]-\int_{0}^{\frac{\pi}{2}}\frac{\sin^{2}t \cancel{\cos t}\ dt}{\cancel{\cos t}}=\textrm{arcsin }1-\int_{0}^{\frac{\pi}{2}}\sin^{2}t\ dt=\textrm{arcsin }1-\int_{0}^{\frac{\pi}{2}}\frac{1-\cos 2t}{2}\ dt=\frac{\pi}{2}-\Big [ \frac{1}{2}t-\frac{1}{2}\cdot \frac{1}{2}\sin 2t \Big ]_{0}^{\frac{\pi}{2}}=\frac{\pi}{2}-\left ( \frac{\pi}{4}-\frac{1}{4}\sin \pi-0+ \frac{1}{4}\sin 0 \right ) =\frac{\pi}{2}-\frac{\pi}{4}=\frac{\pi}{4}}\)
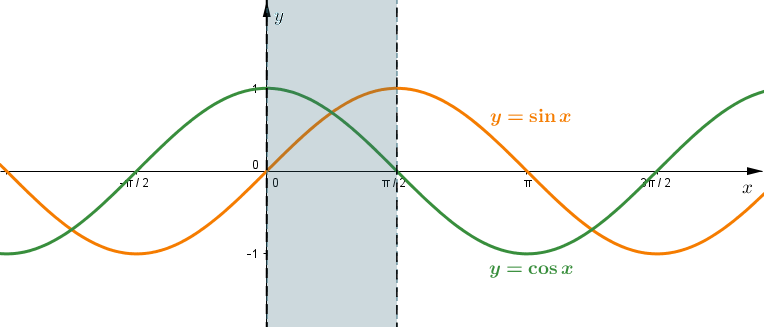
\(\color{#F57C00}{(^{*})(^{**})}\) - odczytujemy z wykresu granice całkowania (\({\displaystyle \sin 0 = 0, \ \sin \frac{\pi}{2}=1}\)) oraz sprawdzamy, że w danych granicach funkcja cosinus jest dodatnia, zatem \(\sqrt{\cos^{2}t}=\cos t.\)
\({\displaystyle =\int_{0}^{1}\frac{1-(x-1)^{2}}{\sqrt{1-(x-1)^{2}}}\ dx=\int_{0}^{1}\frac{dx}{\sqrt{1-(x-1)^{2}}}-\int_{0}^{1}\frac{(x-1)^{2}}{\sqrt{1-(x-1)^{2}}}\ dx=\begin{vmatrix}
x-1=\sin t\\
dx=\cos t\ dt
\end{vmatrix}=\Big[ \textrm{arcsin }(x-1) \Big ]_{0}^{1}-\int_{-\frac{\pi}{2}\color{#F57C00}{(^{*})}}^{0} \frac{\sin^{2}t\cos t\ dt}{\sqrt{1-\sin^{2}t}}=\Big[ \textrm{arcsin }0-\textrm{arcsin }(-1) \Big ]-\int_{-\frac{\pi}{2}}^{0}\frac{\sin^{2}t \cos t\ dt}{\cos t \color{#F57C00}{(^{**})}}=\Big[ 0+\textrm{arcsin }1 \Big ]-\int_{-\frac{\pi}{2}}^{0}\frac{\sin^{2}t \cancel{\cos t}\ dt}{\cancel{\cos t}}=\textrm{arcsin }1-\int_{-\frac{\pi}{2}}^{0}\sin^{2}t\ dt=\textrm{arcsin }1-\int_{-\frac{\pi}{2}}^{0}\frac{1-\cos 2t}{2}\ dt=\frac{\pi}{2}-\Big [ \frac{1}{2}t-\frac{1}{2}\cdot \frac{1}{2}\sin 2t \Big ]_{-\frac{\pi}{2}}^{0}=\frac{\pi}{2}-\left [0- \frac{1}{4}\sin 0 -\left ( -\frac{\pi}{4}-\frac{1}{4}\sin (-\pi) \right ) \right ] =\frac{\pi}{2}-\frac{\pi}{4}=\frac{\pi}{4}}\)
\(\color{#F57C00}{(^{*})(^{**})}\) - odczytujemy z wykresu granice całkowania (\({\displaystyle \sin 0 =1-1=0 , \ \sin \left ( -\frac{\pi}{2}\right )= 0-1=-1}\)) oraz sprawdzamy, że w danych granicach funkcja cosinus jest dodatnia, zatem \(\sqrt{\cos^{2}t}=\cos t.\)
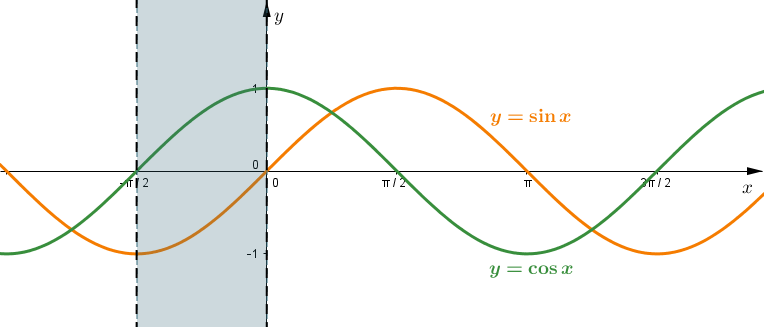
\({\displaystyle =\Big[ x\Big ]_{0}^{1}=1-0=1 }\)
Zatem wracając do pola obszaru \(|P|\) oraz wstawiając wyżej uzyskane całki, otrzymamy:
\[{\displaystyle |P|=\int_{0}^{1}\left [\sqrt{1-x^{2}}-\left (\sqrt{1-(x-1)^{2}}+1 \right ) \right ]\ dx=\int_{0}^{1}\left [\sqrt{1-x^{2}}+\sqrt{1-(x-1)^{2}}-1 \right ]\ dx=\int_{0}^{1}\sqrt{1-x^{2}}\ dx+\int_{0}^{1} \sqrt{1-(x-1)^{2}}\ dx- \int_{0}^{1} 1\ dx =\frac{\pi}{4}+\frac{\pi}{4}-1=\frac{\pi}{2}-1 }\]

