Zadanie 3.4.1.1
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.4. Proste układy mechaniczne
  4. 3.4.1 Nauka
  5. Zadanie 3.4.1.1

 Zadanie 3.4.1.1

Siła pomiędzy ciałami
Trzy stykające się klocki o masach \(m_1=100\ \mathrm{g}\), \(m_2=300\ \mathrm{g}\) i nieznanej masie \(m_3\) leżą na idealnie gładkim stole. Do pierwszego z nich przyłożono siłę o wartości \(10\,\mathrm{N}\). Na skutek działania tej siły, klocki zaczęły poruszać się z przyspieszeniem o wartości \(\displaystyle{2\,\mathrm{\frac{m}{s^2}}}\). Jaka jest wartość siły \(F_{N1}\) i \(F_{N2}\), z którą klocki naciskają na siebie. Ile wynosi masa trzeciego klocka?

 Wskazówka teoretyczna

 Teoria - zasady dynamiki
I zasada dynamiki

W inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.
Zgodnie z  I zasadą dynamiki, suma sił działających na układ musi wynosić zero.

II zasada dynamiki

Jeśli siły działające na ciało nie równoważą się, to ciało porusza się z przyspieszeniem wprost proporcjonalnym do siły wypadkowej, a odwrotnie proporcjonalnym do masy ciała. \[ \vec{a} = \frac{ \sum \vec{F}_{w} } {m} \left[ \frac{m}{s^2} = \frac{N}{kg} \right] \]
III zasada dynamiki

Jeśli ciało \(A\) działa na ciało \(B\) pewną siłą (siłą akcji), to ciało \(B\) działa na ciało \(A\) siłą (siłą reakcji) o takiej samej wartości i kierunku, lecz przeciwnym zwrocie. \[ \vec{F}_{AB} = -\vec{F}_{BA} \]

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa pierwszego klocka \(m_1=100\,\mathrm{g}=0,1\,\mathrm{kg}\),
- masa drugiego klocka \(m_2=300\,\mathrm{g}=0,3\,\mathrm{kg}\),
- siła przyłożona do pierwszego klocka \(F=10\,\mathrm{N}\),
- przyspieszenie obu klocków \(\displaystyle{a=2\,\mathrm{\frac{m}{s^2}}}\).

Szukane:
- wartość siły wzajemnego nacisku klocków \(F_{n1}\),
- wartość siły wzajemnego nacisku klocków \(F_{n2}\),
- masa drugiego klocka \(m_3\).

Analiza sytuacji

 W układzie znajduje się sześć siły działających w kierunku pionowym. Są to: trzy siły nacisku klocków na podłoże \(\vec{P}_1\), \(\vec{P}_2\) i \(\vec{P}_3\) oraz trzy siły reakcji podłoża na nacisk klocków \(\vec{R}_1\), \(\vec{R}_2\) i \(\vec{R}_3\). Zgodnie z III zasadą dynamiki Newtona siły te, przy braku innych działających pionowo sił, wzajemnie się redukują: 
\[ \eqalign{ -\vec{P}_1 &= \vec{R}_1 \\ - \vec{P}_2 &= \vec{R}_2 \\ -\vec{P}_3 &= \vec{R}_3 }\]
Zgodnie z treścią zadania, klocki leżą na „idealnie gładkiej” powierzchni. Oznacza to, że w rozwiązaniu zadaniu, można pominąć tarcie wywołane naciskiem klocków na powierzchnię stołu, gdyż jest ono pomijanie małe.

 Siła zewnętrzna, przyłożona do pierwszego klocka, powoduje ruch wszystkich klocków z tym samym przyspieszeniem \(a\). Ponadto, klocek pierwszy pcha klocek drugi z siłą \(\vec{F}_{n1}\), co zgodnie z III zasadą dynamiki Newtona, wywołuje reakcję w postaci siły \(\vec{F}_{n1}\), z jaką klocek drugi działa na pierwszy. Siły te, co do wartości, są takie same. Sytuacja ta powtarza się pomiędzy klockiem drugim a trzecim. Tym razem występuje inna siła o wartości \(\vec{F}_{n2}\). 

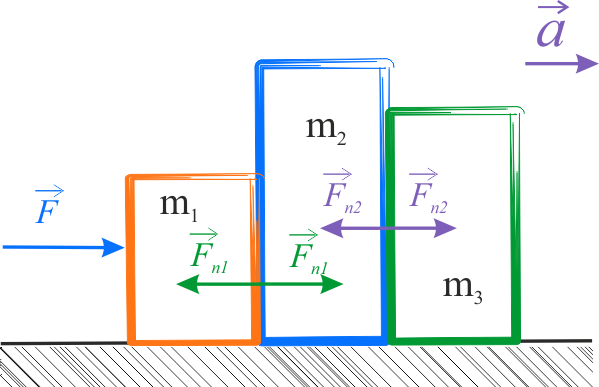
Rysunek


Wykorzystując II zasadę dynamiki Newtona możemy dla trzech klocków napisać równania wiążące siły działające na nie z ich przyspieszeniem. Pisząc równania patrzymy kolejno na jeden, wybrany klocek. Obiekty są trzy, więc równań też będzie trzy.

1.  Na klocek pierwszy działa siła zewnętrzna \(\vec{F}\) oraz siła nacisku od drugiego klocka \(\vec{F}_{n1}\), a ich wypadkowa porusza klocek z przyspieszeniem \(a\). 
\(\vec{F} + \vec{F}_{n1} = m_1 \vec{a}\)

2.  Na drugi klocek działa siła nacisku pierwszego klocka \(\vec{F}_{n1}\) oraz drugiego klocka \(\vec{F}_{n2}\), powodując ruch klocka z przyspieszeniem \(a\). Możemy to zapisać wzorem w postaci wektorowej: 
\(\vec{F}_{n1} + \vec{F}_{n2} = m_2 \vec{a}\)

3.  Na trzeci klocek działa tylko siła nacisku drugiego klocka: 
\(\vec{F}_{n2} = m_3 \vec{a}\)

Powyższe równania można zapisać w sposób skalarny. Wektorom skierowanym w tym samym kierunku, co przyspieszenie układu nadajemy wartość dodatnią, a wektorom skierowanym w lewo - wartości ujemne:

\(\left\{\begin{matrix} a\,m_1= &F-F_{n1}\\ a\,m_2= &F_{n1}-F_{n2}\\ a\,m_3= &F_{n2} \end{matrix}\right.\)

Rozwiązanie

Rozwiązanie zadania wymaga rozwiązania układu równań:

\(\left\{\begin{matrix} a\,m_1= &F-F_{n1}\\ a\,m_2= &F_{n1}-F_{n2}\\ a\,m_3= &F_{n2} \end{matrix}\right.\)

W trzech równaniach mamy trzy niewiadome: \(m_3\), \(F_{n1}\) i \(F_{n2}\), co pozwala na rozwiązanie zadania.
Otrzymane równania przekształcamy do postaci:

\(\left\{\begin{matrix} F_{n1}= &F-a\,m_1\\ F_{n2}= &F_{n1}-a\,m_2 \\ m_3= &\Large{\frac{F_{n2}}{a}} \end{matrix}\right.\)

Teraz wystarczy podstawić wartości liczbowe i otrzymamy odpowiedź do zadania.

\(\left\{\begin{matrix} F_{n1}= &10-2\cdot 0,1=9,8\,\mathrm{N} \\ F_{n2}= &9,8-2\cdot 0,3=9,2\,\mathrm{N} \\ m_3= &\frac{9,2}{2}=4,6 \,\mathrm{kg} \end{matrix}\right.\)

Zobaczmy jak zmienia się nacisk pomiędzy poszczególnymi klockami w przypadku, gdy mają one taką sama masę \(m=2\,\mathrm{kg}\). Przyjmijmy do obliczeń, że \(F=12\,\mathrm{N}\), a przyspieszenie \(\displaystyle{a=2\,\mathrm{\frac{m}{s^2}}}\).
Układ równań wygląda następująco:

\(\left\{\begin{matrix} a\,m= &F-F_{n1} \\ a\,m= &F_{n1}-F_{n2} \\ a\,m= &F_{n2} \end{matrix}\right.\)

Siły nacisku wynoszą:

\(\left\{\begin{matrix} F_{n1}= &F-a\,m=12-2\cdot 2=8\,\mathrm{N} \\ F_{n2}= &F_{n1}-a\,m=8-2\cdot 2=4\,\mathrm{N} \end{matrix}\right.\)

Z obliczeń wynika, że na ostatni klocek działa najmniejsza siła. Siły działające pomiędzy sąsiednimi klockami nie maja takiej samej wartości \(F_{n1}\neq F_{n2}\).

Odpowiedź

Wartości sił nacisku klocków wynoszą \(F_{n1}=9,8\ \mathrm{N}\) oraz \(F_{n2}=9,2\ \mathrm{N}\), a masa trzeciego klocka ma wartość \(4,6\ \mathrm{kg}\).