Zadanie 4.4.1.1
  1. Kurs obliczeniowy z fizyki
  2. 4. Praca, moc, energia, pęd
  3. 4.4. Zasada zachowania pędu
  4. 4.4.1 Nauka
  5. Zadanie 4.4.1.1

 Zadanie 4.4.1.1

Pęd ciała
Na rysunku przedstawiono zależność od czasu siły działającej na ciało o masie \(0,5\,\mathrm{kg}\) poruszające się po linii prostej. Wyznacz zmianę pędu po \(6\,\mathrm{s}\).

 Wskazówka teoretyczna

 Teoria - uogólniona postać drugiej zasady dynamiki
Uogólniona postać drugiej zasady dynamiki, w której korzysta się z definicji pędu ciała \(\vec{p}=m\,\vec{v}\), wyrażona jest wzorem:

\(\displaystyle{\vec{F}=\frac{\mathrm{d}\vec{p} }{\mathrm{d}t} }\)
Rysunek

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa poruszającego się ciała \(m=0,5\,\mathrm{kg}\),
- czas, po jakim należy wyznaczyć zmianę pędu ciała \(t=6\,\mathrm{s}\),
- zależność siły działającej na ciało od czasu \(F(t)\).

Szukane:
- zmiana pędu ciała po czasie \(t\): \(\Delta p\).

Analiza sytuacji

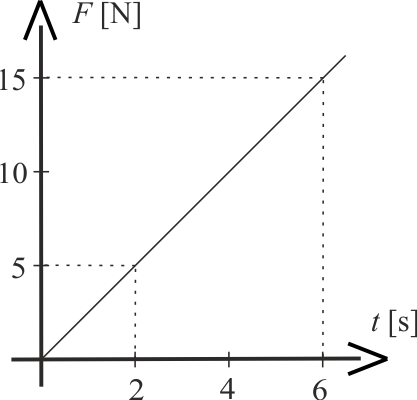
Z wykresu widzimy, że na ciało działa siła, której wartość rośnie proporcjonalnie do czasu. Do wyznaczenia zmiany pędu ciała zastosujmy uogólnioną postać II zasadę dynamiki oraz graficzną interpretację zmiany pędu ciała pod wpływem siły zależnej od czasu.

\(\displaystyle{F=\frac{\mathrm{d}p}{\mathrm{d}t}}\),

a zmianę pędu ciała można wyznaczyć jako:
\(\displaystyle{\Delta p=\int_0^t F\,\mathrm{d}t}\)

Na podstawie wykresu można wyznaczyć zależność \(\displaystyle{F(t)=\frac{5}{2}t\,\mathrm{\left [\frac{N}{s}\cdot s\right ]} }\)

Sposób 1

Na wykresie zaznaczone są dwa punkty \(\displaystyle{A=(2,5)\,\mathrm{\frac{N}{s}}}\) oraz \(\displaystyle{B=(6,15)\,\mathrm{\frac{N}{s}}}\). Na podstawie ich współrzędnych wyznaczamy równanie prostej \(y=ax+b\).

\(\begin{eqnarray} \begin{cases} 5 &=2a+b\\ 15 &=6a+b \end{cases} \end{eqnarray} \)

Po odjęciu stronami od równania drugiego pierwsze, mamy:

\(10=4a\)
\(\displaystyle{a=\frac{5}{2}}\)

Współczynnik \(b\) wynosi zero, więc ostatecznie otrzymujemy zależność \(\displaystyle{F(t)=\frac{5}{2}t\,\mathrm{\left [\frac{N}{s}\cdot s\right ]} }\)

Sposób 2

Prosta przedstawiona na wykresie przechodzi przez początek układu współrzędnych więc współczynniki \(b\) wynosi zero, a zatem prosta będzie miała postać \(y=ax\). Współczynnik kierunkowy prostej \(a\) można wyznaczyć, jako tangens kąta nachylenia tej prostej do osi \(x\), czyli:

\(\displaystyle{a=\operatorname{tg}{\alpha}=\frac{5}{2}}\)

Ostatecznie otrzymujemy \(\displaystyle{F(t)=\frac{5}{2}t\,\mathrm{\left [\frac{N}{s}\cdot s\right ]} }\)

Rozwiązanie

1. Sposób rozwiązania.

Na wykresie, pole powierzchni pod krzywą, przedstawiające zależność siły od czasu, jest równe całkowitej zmianie pędu ciała. Ponieważ z wykresu mamy, że \(F(6)=15\,\mathrm{N}\) to:

\(\displaystyle{\Delta p=\frac{1}{2}\cdot 6\,\mathrm{s}\cdot 15\,\mathrm{N}=45\,\mathrm{Ns} }\)
\(\displaystyle{\Delta p=45\,\mathrm{kg\,\frac{m}{s}} }\)
2. Sposób rozwiązania.

Z wykresu znajdujemy analityczną postać zależności siły od czasu \(\displaystyle{F(t)=\frac{5}{2}t\,\mathrm{\left [\frac{N}{s}\cdot s\right ]} }\), a następnie wykonujemy całkowanie

\(\displaystyle{\Delta p=\int_0^t F\,\mathrm{d}t=\int_0^6 \frac{5}{2}t\,\mathrm{d}t }\)

\(\displaystyle{\Delta p=\frac{5}{2}\cdot \frac{1}{2}\left [t^2\right ]_0^6 }=45\)

\(\displaystyle{\Delta p=45\,\mathrm{kg\,\frac{m}{s}} }\)

Odpowiedź

Zmiana pędu po \(6\,\mathrm{s}\) wynosi \(\displaystyle{\Delta p=45\,\mathrm{kg\,\frac{m}{s}} }\).