
1.1. Identification Schemes and Introduction to interactive proof systems
Verification whether someone is who he claims to be.
- Biometric
- Passwords
- Legal Documents
- Cryptographic identification schemes (we focus on these)
Parties
- Prover \( P \) - has a private key \(SK_P\) and a public key \(PK_P\).
- Verifier \( V \) - having \(PK_P\) outputs ,,accept'' or ,,reject'' after an interaction with the prover \(P\).
Security
- Correctness - if \(P\) knows the corresponding secret key, then \(V\) returns ,,accept'' with overwhelming probability.
Types of Cryptographic Identification Schemes
- Interactive
- Non-Interactive (e.g. signature schemes)
Notation
- \( R\) - binary relation for pairs \((s ,w) \in R\), consisting of a statement \(s\) and a witness \(w\).
- \(L_R\) - NP-language of statements \(s\) that have witnesses \(w\) of length \(k\) in \(R\) i.e \( \{s : \exists_{w, |w| = k} \land (s, w)\in R \} \)
- \(w(s)\) - set of all witnesses to the statement \(s\)
Definition
A pair of algorithms \((P, V)\) is a proof system if it satisfies
- Correctness - for all \(s \in L_R\) and \(w \in w(s)\), the probability that \(V_P(s,w)(s) = 1\) is \(1 - \epsilon\).
- Soundness - For all \(x \in L_R\) (false statements) the probability that \(V_P(s,w)(s) = 1\) is \( \epsilon\).
Encryption Scheme
- User has a secret key \(SK\) and public key \(PK\).
- \(c \rightarrow Enc_{PK}(m)\).
- \(m \rightarrow Dec_{sk}(c)\).
Proving the ability to decrypt a ciphertext
- Verifier chooses a random \(r\) and encrypts it \(c \rightarrow Enc_{PK}(r)\).
- Prover decrypts \(r \rightarrow Dec_{SK}(c)\) and shows the decryption to the verifier.
Soundness - Yes.
Proof of Knowledge of Discrete Logarithm
- \(Y = g^x\) - Statement is the knowledge of \(Log_{g}(Y)\).
- The witness set is \(w(s) = \{x\}\).
- Prover simply shows \(x'\).
- Verifier accepts if \(g^x \stackrel{?}{=} Y\).
Properties
- Correctness - if \(x'\) is the discrete logarithm, then the verifier accepts.
- Soundness - if \(x'\) is not the discrete logarithm, then the verifier rejects.
Definition
A proof system is a Proof of Knowledge if for all \(s \in L_R\), \(V_{P^*}(s) = 1\) and there exists an extractor \(E(x; P^*) \in w(x)\) with probability \(1 - \epsilon\).
Question
- Does the surprising example have a extractor?
- Does the proof system utilizing a encryption scheme has a extractor?
- Zero-Knowledge - give no knowledge on the witness
- Witness-Indistinguishability - it is infeasible to tell for which witness the proof is made
- Witness-Hiding - it is infeasible to compute the witness from the proof
Implication
\[ \mathrm{ZK} \Rightarrow \mathrm{WI} \Rightarrow \mathrm{WH} \]
Along this lecture we focus on ZK
Definition
Proof system \((P, V)\) is zero knowledge over the relation \(R\) if there exists a simulator \(M\) which such that for any probabilistic polynomial time \(V'\), for any \((s, w) \in R\), and any auxiliary input \(y\) to \(V'\) the two ensembles \(V_P(s, w)'(s, y)\) and \(M(s, y; V')\) are indistinguishale.
Proof of Knowledge of Discrete Logarithm
Prover wants to prover the knowedlge of \(Log_{g}(Y)\).
- Prover chooses \(t \in \mathbb{Z}_p\) at random and sends \(T \rightarrow g^t\) to the verifier.
- Verifier chooses \(c \in \mathbb{Z}_p\) at random and sends \(c\) to the prover.
- Prover computes \(\sigma \leftarrow t + c \cdot x\).
- Verifier accepts if \(T \stackrel{?}{=} g^{\sigma}Y^{-c}\) holds.
Correctness
If \(Y = g^x\), then \(g^{\sigma}Y^{-c} = g^{t}\cdot g^{c \cdot x} \cdot g^{-c \cdot x} = g^t = T\).
Proof of Knowledge (existence of an extractor)
- Suppose we can rewind the Prover to the moment he obtains \(c\).
- We send another \(c' \neq c\).
- The prover computes \(\sigma' \leftarrow t + c' \cdot x\).
- Now we have \(\sigma\) and \(\sigma'\) which satisfy
- \(T = g^{\sigma}Y^{-c} = g^{\sigma'}Y^{-c'}\)
- Thus we simply obtain \(x = (\sigma - \sigma')/(c - c')\).
Soundness
Suppose a prover wants to prove a false statement (i.e. the prover don't knows \(Log_{g}(Y)\)). In case he is successful, we run the extractor and extract \(Log_{g}(Y)\) while interacting with him. Thus, the prover has to know \(Log_{g}(Y)\) and the statement couldn't be false. Moreover, a prover having an algorithm which produces a convincing proof, could use the extractor by himself.
Honest verifier, public coin Zero Knowledge
Simulation
- We chose \(\sigma\) and \(c\) at random and compute
- \(T \leftarrow g^{\sigma} \cdot Y^{-c}\).
\(\Sigma\)-Protocols
\(\Sigma\)-protocols are a generalization of proof systems as Schnorr or Okamoto protocols. We call a \(\Sigma\)-protocol, a protocol between a prover \(P\) and a verifier \(V\) of the form:

Properties
A \(\Sigma\)-protocol satisfies the following properties:
- Correctness - If \(P\) and \(V\) follow the protocol, then \(V\) accepts.
- Special soundness - there exists an extractor \(E\) which given any pair of accepting conversations \((T, c, r)\) and \((T, c', r')\) where \(c \neq c'\) computes a witness \(w\) satisfying \((s, w) \in R\).
Types of composition
- AND
- EQ
- OR
- NEQ
AND composition
Prover wants to prove the knowledge of \(Log_g(Y_1)\) AND \(Log_g(Y_2)\).
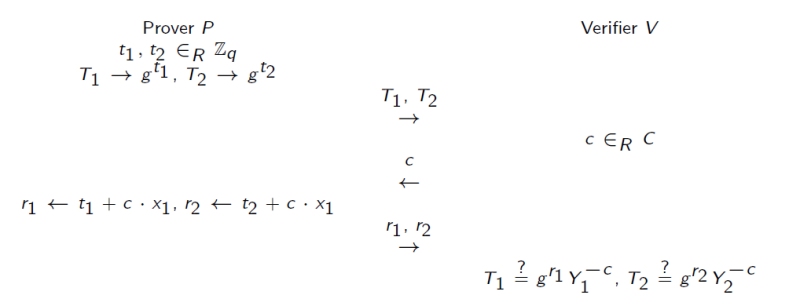
EQ composition
Prover wants to prove the knowledge of \(x = Log_{g_1}(Y_1) = Log_{g_2}(Y_2)\).

OR composition
Prover wants to prove the knowledge of \(x = Log_{g_1}(Y_1) = Log_{g_2}(Y_2)\).

NOT composition
Prover wants to prove the knowledge of \(x_1 = Log_{g_1}(Y_1) \neq x_2 = Log_{g_2}(Y_2)\).

Simplified notation - example
\[PoK\{(\alpha, \beta): g^{\alpha} = y \land \hat{g}^{\alpha}g^{\beta} = z\}\] This denotes a proof of knowledge protocol for the knowledge of \(\alpha\) and \(\beta\) s.t. the relations \(g^{\alpha} = y\) and \(\hat{g}^{\alpha}g^{\beta} = z\) hold.