• Master key, from which encryption keys are derived allows to store only \(1\) key to have access to each file, however after deletion of one file, new master key has to be created in order to properly protect the deleted file.
• Individual keys for each file allow easy file deletion, however the data owner has to store all the keys.
• Key modulation allows both: small client storage overhead and small deletion overhead.

Having master key \(K\) and a set of \(M\) values called modulators one can derive data keys for many files.
Each data key \(k\) is calculated using a one-way function \(F\): \[k:=F(K,\,M_k),\] where \(M_k\) is a unique subset of \(M\) The master key is stored at the client, while the modulators are stored in the cloud, unencrypted. To delete \(k\) the client will permanently delete \(K\) and choose a new master key \(K'\) In addition, it will adjust the values of \(O(\log n)\) modulators in \(M\setminus M_k\) such that all other data keys \(k'\) stay the same, i.e., \(k'=F(K',M'_{k'})=F(K,M_{k'})\) where \(M_{k'}\) is the subset of modulators for \(k'\) before deletion and \(M'_{k'}\) is the same subset after deletion (with one modulator having a new value). For the deleted key \(k\) since we do not change any modulator in \(M_k\) \(F(K,M_k)\neq F(K',M_k)\) Therefore, even if the new master key \(K'\) is compromised in the future, the deleted key \(k=F(K,M_k)\) is not recoverable after \(K\) is permanently deleted.

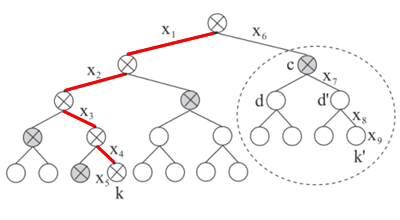
All modulators are organized in a tree structure. Before outsourcing a file of \(n\) data items to the cloud, the client randomly picks a master key \(K\) and then builds a modulation tree, which is a complete binary tree with each leaf node representing a data key.
Let \(P(k)\) be the path from the root to node \(k\). The client turns the link modulators along the path and the leaf modulator at the end of the path into an ordered list \(M_k\), and computes a data key \(k=F(K,M_k)\) by applying the modulated hash chain.

Fig. 5.4.4/1

Fig. 5.4.4/1 comes from   : 1 .
A modulation tree, where each leaf node is assigned a leaf modulator such as \(x_5\), and each link is assigned a link modulator such as \(x_1\) through \(x_4\). The path \(P(k)\) from the root to the leaf node \(k\) is drawn in red lines; it is a graphical representation of \(M_k=\left< x_1,x_2,x_3,x_4,x_5 \right >\). The nodes in the cut \(C\) are shaded. \(M_x=x_6\) is a prefix of \(M_{k'}\) for any leaf \(k'\) in the sub-tree rooted at \(c\).

Results presented by the authors in   : 1 

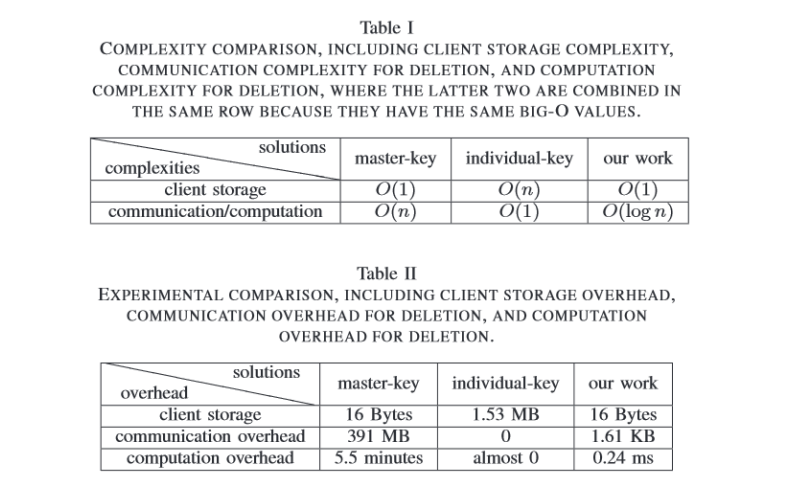
Fig. 5.4.4/2: Results