• Introduced first by Chaum and Van Heyst in ,,Security Without Identification: transaction systems to make big brother obsolete''.
• In group signatures we have the following parties:
  • Group manager - creates the group verification key and adds users to the group.
  • Group members (users) - may create a signature on behalf of the group.
• Basically, we want that:
  • Only group members may sign on behalf of the group.
  • A signature discloses only information about the group membership. So, a verifier having two signatures cannot determine whether the signatures where produced by two distinct users or one user.
  • We want also an opening algorithm.

Security Properties

• Correctness - verifier accepts a signature produced by an honest group member.
• Full-Frameability - the adversary goal is to produce a valid signature, having access to a set of group secret keys, which opens to a identity outside the the set.
• Full-Traceability - the adversaries goal is to produce a signature which verifies correctly but for which the opening procedure fails.
• Full-Anonymity - the adversary has access to all group secret keys, chooses two identities and in the challenge phase obtains a signature from one identity of his choice. The adversaries goal is to guess the identity of the signer.

Key generation

1. Compute a common reference string \(\rho \leftarrow K(1^k)\)
2. Compute the private/public key pair \((SK_s, PK_s) \leftarrow \Sigma.Kg(1^k)\) for the digital signature scheme \(\Sigma\)
3. Compute the private/public key pair \((SK_e, PK_e) \leftarrow \Omega.Kg(1^k)\) for the public key encryption scheme \(\Omega\)
4. For \(i = 1\) to \(n\): compute \((sk_i, pk_i) \leftarrow \Sigma.Kg(1^k)\) and \(cert_i \leftarrow Sign(sk_s, (i, pk_i))\).
5. Output:
   • group public key \(gpk = (\rho, PK_s, PK_e)\)
   • group managers secret key \(gmsk = (gpk, sk_e)\)
   • secret key for member \(i\): \(gsk[i] = (gpk, sk_i, pk_i, cert_i)\)

Signature generation (\(gsk[i], M\))

1. Compute \(s \leftarrow Sign(sk_i, M)\) and \(c \leftarrow Enc(pk_e, (i, pk_i, cert_i, s))\)
2. Compute \(\pi\) as a non-interactive zero-knowledge proof of knowledge: \[ \begin{equation*} \begin{split} NIZKPoK\{ i, pk_i, cert_i, s: Verify(pk_s, (i, pk_i), cert_i)=1 &\land \\ Verify(pk_i, m, s)=1 &\land \\ Enc(pk_e, (i, pk_i, cert_i, s)=c \} \end{split} \end{equation*} \]
3. Output group signature \((\pi, c)\)

Verify Signature

• If \( \pi\) is a valid NIZKPoK then output ,,accept'', otherwise output ,,reject''

Signature generation(\(gsk[i], M\))

1. Compute \(s \leftarrow Sign(sk_i, M)\) and \(c \leftarrow Enc(pk_e, (i, pk_i, cert_i, s))\)
2. Compute \(\pi\) as a non-interactive zero-knowledge proof of knowledge: \[ \begin{equation*} \begin{split} NIZKPoK\{ i, pk_i, cert_i, s: Verify(pk_s, (i, pk_i), cert_i)=1 &\land \\ Verify(pk_i, m, s)=1 &\land \\ Enc(pk_e, (i, pk_i, cert_i, s)=c \} \end{split} \end{equation*} \]
3. Output group signature \((\pi, c)\)

Open

1. Verify the signature
2. Decrypt \((i, pk_i, cert_i, s) \leftarrow Dec(sk_e, c)\)

Current state of the art

• Available RSA, DL, Bilinear and Latice based constructions
• Constant time of signing, verifying and opening
• Revocation simply by creating a new group
• Other revocation notions are accumulators or revocation lists.
• Decentralization of the issuer or opening
• Group signatures with verifiable opening

Group Signatures - further challenges

• VLR signature needs linear time for revocation
• Forward secure group signatures
• We have efficient construction, but not necessarily for resource constrained devices
• many more....

Concept

Sample use case

Parties

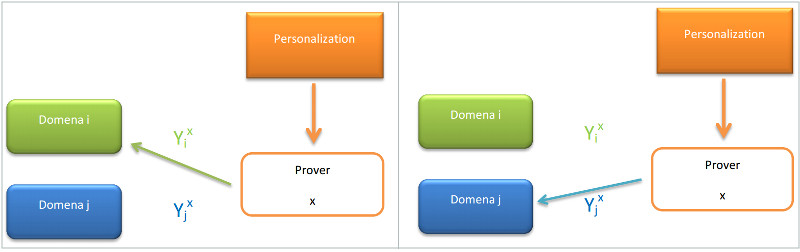
• Domains - domain \(j \) has a legal name \(A_j \in \{0, 1\}^*\).
• Users - have a secret key \(x\) and a corresponding public key \(x, g^x\).
• Issuer - Issues certificates for user pseudonyms.
  1. A user with private key \(x\) computes a domain specific pseudonym as \(Y \leftarrow H(A_j)^x\).
  2. The issuer issues a certificate for that pseudonym \(Cert_{Issue}(Y)\).

Signature generation for message \(M\)

1. Choose \(t\) at random and computes \(T \leftarrow H(A_j)^t\).
2. Compute the challenge \(c \leftarrow H(T, M)\) and \(s \leftarrow t + c \cdot x\).
3. The signature for domain \(j\) and pseudonym \(Y = H(A_j)^x\) with certificate \(Cert(Y)\) is \(\sigma = (c, s)\).