
5.2. Processing of sensitive information in clouds
According to : 9 even with full confidence in cloud-supplied layers, cloud security engineering requires careful teamwork between the outsourcing vendor and the customer. The security featured of vendor -supplied layers and customer-supplied layers must mesh without a flaw when they are used to implement a solution together. Moreover, as it stays in : 7 public clouds are threatened by hackers due to the much larger target they present. Owners of sensitive data must take into account also other participants in cloud ecosystem - cloud neighbors and administrators. Insiders such as data center administrative staff can easily access private data that has been outsourced. Such attacks are realistic and have already been reported. In several publish attacks one stage of the attack is becoming the cloud neighbor of the target (see : 11 ) Thus users should take precautions to ensure the confidentiality and privacy of their sensitive cloud data.
Pre-transmission data encryption scenario
Probably the best from the data confidentiality point of view is pre-transmission data encryption. In this scenario one has to:
- encrypt each dataset prior to its transmission to the cloud and
- decrypt it upon retrieval from the cloud.
Such a solution has however one serious drawback - outsourcing the management of huge datasets and downloading the entire dataset each time before use is simply impractical. In case of databases we often have queries which return relatively small (to the size of the whole database) results. Here instead of returning a small answer, first the entire database would need to be download.
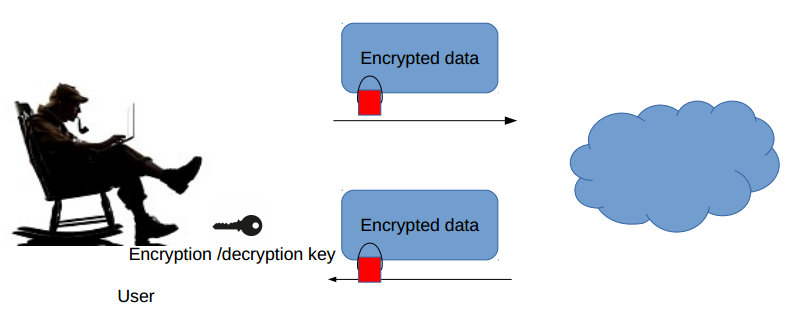
Fig. 5.2/1: Pre-transmission data encryption
Data at rest encryption scenario
In cloud based storage systems we can use so called data at rest encryption. In this scenario data:
- is encrypted when stored to any cloud storage service and
- decrypted when requested by any application.
Such a solution allows computation over the data and is especially useful against physical attacks (like stolen disk drive). Unfortunately it does not protect data in use and requires a decryption key to be stored in the cloud. As it stays in : 9 many attacks are aimed exactly at obtaining the decryption key. Furthermore the moment the query hits a cloud application, data is decrypted and brought into the cloud memory as plaintext. Thus the attackers do not actually need to obtain the key to defeat data at rest encryption (they simply need to exfiltrate plaintext from cloud memory).
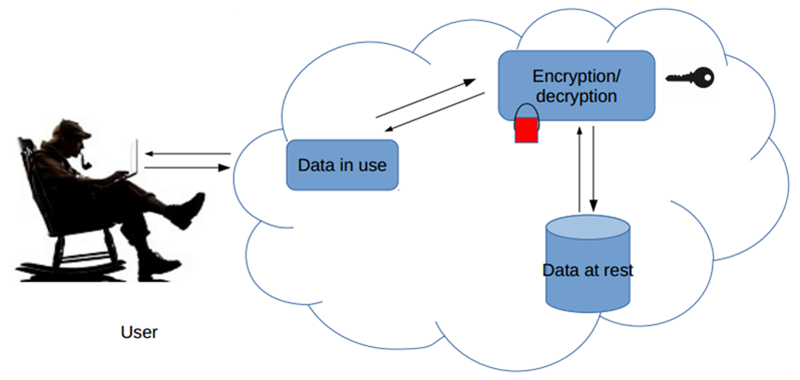
Fig. 5.2/2: Data at rest encryption.
According to : 9 homomorphic cryptosystems promise the best of two worlds:
- The ability to expose neither plaintext data nor decryption keys in clouds.
- The ability for applications to nonetheless compute over encrypted data while it resides in the remote cloud.
Cryptosystems
Cryptosystems are valued primarily for their ability to secure information. As a side-effect, however, operations on their corresponding ciphertexts in some cryptosystems correspond to useful operations on plaintexts, which is called a homomorphism. For example:
- Pailier cryptosystem (see Pailier in Additional materials) is additively homomorphic, because: \[E(m_1) \cdot E(m_2) = E(m_1 + m_2)\]
- RSA cryptosystem is multiplicatively homomorphic, because: \[E(m_1) \cdot E(m_2) = m_1^d\cdot m_2^d = (m_1\cdot m_2)^d = E(m_1 \cdot m_2) \]
- ElGamal cryptosystem is multiplicatively homomorphic, because: \[E(m_1) \cdot E(m_2) = \\ (m_1 \cdot y^{r_1}, g^{r_1}) \cdot (m_2 \cdot y^{r_2}, g^{r_2}) = (m_1 \cdot m_2 \cdot y^{r_1+r_2}, g^{r_1+r_2}) = E(m_1 \cdot m_2) \]
The question naturally arises as to whether any cryptosystem is fully homomorphic?
Fully homomorphic cryptosystem definition
We call the cryptosystem fully homomorphic if it enables any computable operation to be performed over plaintexts using ciphertext dataset.
The fully homomorphic encryption problem (FHE) was an open problem for over 30 years. In 2009 Craig Gentry : 5 proposed a fully homomorphic and semantically secure cryptosystem. Its performance degrades sharply with its security parameter (performance is estimated to be as bad as 10 orders of magnitude worse than the corresponding plaintext operations; such that one second computation would take over three centuries!). Although the research on FHE is now very active we should have in mind that an efficient FHE implementation would not immediately enable users to execute conventional queries in cloud based Databases.
Even if we assume that encryption of data at rest gives data confidentiality, it is worth to stress that it is not sufficient in the field of privacy. Namely, the subsequent data access patterns can leak information about the user. Thats why retrieval of sensitive data from databases or web services, such as medical databases or patent databases implies concerns on user privacy exposure. For example, if the outsourced data in question contains encrypted patient records, the cloud provider might learn that a patient has been diagnosed with cancer when it sees that the patient's records have been retrieved by an oncologist. In general, it is hard to assess which information may be leaked, what inferences an adversary may make, and what risks the leakage may incur. Solutions to the information leakage problem that hide access patterns and are independent of an encryption mechanism offer private information retrieval (PIR) schemes.
The goal of PIR
The goal of Private Information Retrieval (PIR) is to allow a client to successfully query a database in such a way that no one, including the database operator, can determine which records of the database the client is interested in.
Many PIR schemes have been developed so far. Interested readers are referred to a survey : 4 for a thorough review. Generally, depending on whether the scheme utilizes some trusted hardware or not, the PIR schemes can be divided into two categories:
- traditional PIR schemes and
- hardware-based PIR schemes.
Another classification divides PIR protocols into:
- those that provide privacy guarantees based on the computational limitations of servers (CPIR),
- those that rely on multiple servers not colluding for privacy (IT-PIR).
Trivial download
The simplest approach to PIR, called trivial download, is for the user to request the
entire database from the server.
Downloading the whole data \(D\) for every check is very costly!
What is PIRMAP?
A PIRMAP (originally described in : 7 ) is CPIR protocol particularly suited to MapReduce (see MapReduce in Additional materials) - a widely used cloud computing paradigm. PIRMAP focuses especially on the retrieval of large files from the cloud, where it achieves good communication complexity. It runs on top of standard MapReduce, not requiring changes to the underlying cloud infrastructure.
Authors of : 7 have implemented (the source code is available for download from http://pasmac.ccs.neu.edu PIRMAP that is usable in real-world MapReduce clouds today, e.g., Amazon. They evaluated PIRMAP, first, in their own (tiny) local cloud and, second, with Amazon's cloud. They also verified its practicality by scaling up to 1 TByte of data in Amazon's cloud setting. PIRMAP can be used with any additively homomorphic encryption scheme.
PIRMAP details
As it stays in : 7 PIRMAP assumes that the cloud user has already uploaded its files into the cloud using the interface provided by the cloud provider. Thus during the query procedure we get the following assumptions: data set holds \(n\) files, each of \(l\) bits length (to accommodate variable length files the padding should be used). Additional parameter \(k\) specifies the block size of a cipher utilized. PIRMAP is summarized as follows:
- User side: if the user wishes to retrieve file \(1 \leq x \leq n\), he executes Query:
- creates a vector \(v = (v_1, \ldots, v_n)\), where:
- \(v_x = E(1)\)
- \(\forall_{i \neq x}{v_i = E(0)}\) and
- \(E\) denotes additively homomorphic encryption scheme,
- sends \(v\) to the MapReduce cloud.
- creates a vector \(v = (v_1, \ldots, v_n)\), where:
- Cloud side:
- Each mapper nodes evaluates Multiply on its locally stored file \(i\):
- the file \(i\) is divided into \(\frac{k}{l}\) blocks \(\{B_{i,1} ,\ldots , B_{i,\frac{l}{k}}\}\),
- each block is multiplied by \(v_i\),
- the following key-values pairs are generated for the reducer \( (1, v_i \cdot B_{i,1}), \ldots, (1, v_i \cdot B_{i,\frac{l}{k}}) \).
- Reducer evaluates Sum: all values with the same key are added.
- One result vector of values \(r = (r_1, \ldots, r_{\frac{l}{k}})\) is sent to the user.
- Each mapper nodes evaluates Multiply on its locally stored file \(i\):
Summarizing, in PIRMAP protocol the cloud arranges \(n\) files into a following table \(T\): \[ \begin{array}{c | c c c c} & 1 & 2 & \ldots & \frac{l}{k}\\ \hline \\ file_1 & B_{1,1} & B_{1,2} & \ldots & B_{1, \frac{l}{k}}\\ file_2 & B_{2,1} & B_{2,2} & \ldots & B_{2, \frac{l}{k}}\\ \ldots & & & \ldots & \\ file_n & B_{n,1} & B_{n,2} & \ldots & B_{n, \frac{l}{k}} \end{array} \] Then the cloud performs the vector-matrix multiplication: \(r = v \cdot T\). The user receives \(\frac{l}{k}\) values of size \(k\) and decrypts it to get \(file_x\).
Encryption of PIR values
Map phase of PIRMAP protocol involves multiplying every piece of the data set by an encrypted PIR value. Thus it is important that we choose an efficient cryptosystem.
- traditional additively homomorphic cryptosystems, such as Paillier's (see Pailier in Additional materials) allow for elements \(a\) and \(b\) to compute \(E(a)\cdot E(b) = E(a + b)\). Since map phase consists of multiplying ciphertexts by unencrypted scalars, we would have to do exponentiation of a ciphertext. PIRMAP, and all PIR schemes, must compute on the whole data set, so this step would be computationally intensive
- it might be better to use a somewhat homomorphic encryption scheme introduced by Trostle and Parrish : 10 .
This scheme encrypts \(n\) bits with security parameter \(k > n\) as follows:
-
- KeyGen(\(1^k\))
- Generate a prime \(m\) of \(k\) bits and a random \(b < m\); \(b\) and \(m\) are secret.
- Encrypt
- \(E(x) := b \cdot (r \cdot 2^n + x) \mbox{ mod } m\) for a random \(r\).
- Decrypt
- \(D(c) := b - 1 \cdot c \mbox{ mod } m \mbox{ mod }2^n\).
-
PIRMAP privacy
Privacy-preserving PIRMAP
According : 7 PIRMAP is privacy-preserving, iff an adversary (the cloud) cannot guess, after each query, with probability greater than \(\frac{1}{n}\), which file was retrieved by the userafter an invocation of the protocol.
There are two pieces of information that the adversary has access to:
- the set of uploaded files and
- the vector \(v\) of PIR values.
PIRMAP advantages and disadvantages
PIRMAP advantage
PIRMAP is an efficient CPIR protocol that exploits the massive parallelism available in cloud computing to split the server's workload on multiple machines using MapReduce. Its communication complexity is \(O(l)\) when retrieving an \(l\) bit file.
PIRMAP disadvantage
PIRMAP requires a "somewhat homomorphic" encryption scheme to be used by the client to hide the contents of the query vector and to decipher the contents of the response from the server. According : 3 this amount of client-side computation is non-trivial and can be avoided using IT-PIR schemes.
As it is summarized in : 3 Goldberg scheme:
- Makes use of Shamir's Secret Sharing to ensure the privacy of fetched information. Suppose we have a secret \(\sigma\) in some field \(F\), then we create a random function \(f\) of degree at most $\(t\) that encodes the secret so that \(f (0) = \sigma\). We then create a set of shares \(\{(\alpha_1, f(\alpha_ 1)), (\alpha_2, f(\alpha_ 2)), \dots, (\alpha_l, f(\alpha_ l))\}\) with \(\alpha_1,\dots , \alpha_l \in F\) and \(\alpha_i \neq 0\) and distribute them to a set of servers. As long as no more than \(t\) of the servers are colluding, none of them will be able to determine the secret.
- Assumes that the database is an \(r \times s\) matrix \(D\) and that each of servers have a copy of \(D\). Each row of the database represents a record. If we want the record at row \(\beta, D_\beta\), we create the elementary vector \(e_\beta = \langle 0, 0, \dots, 1, \dots, 0\rangle \in F^r\), where the \(1\) is in the \(\beta^{\mbox{th}}\) position, and multiply by \(D\): \(D_\beta = e_\beta \cdot D\).
- In order to hide \(\beta\) from the database operators we use Shamir's Secret Sharing to create \(l\) shares of \(e_\beta\): \(v_1, v_2, \dots, v_l \in F^r\), and send query vector \(v_i\) to server \(i\). Each server computes a response vector \(r_i = v_i \cdot D\) and returns it to the client.
- As long as enough servers send their response, the client can recover the database record since \(r_1, r_2, \dots, r_l\) are Shamir's Secret Shares for \(D_\beta\).
- As long as no more than \(t\) servers collude, none of the servers can determine any information about the record that was fetched.
Goldberg IT-PIR scheme advantage
According to : 2 , the client-side computation required for this scheme can be done very quickly.
Goldberg IT-PIR scheme disadvantage
The bottleneck of this scheme is vector-by-matrix multiplication on the server's side. But ... as it was shown in : 3 this operation can be easily parallelized, what significantly improves the performance of scheme.
As it stays in : 3 the vector-by-matrix multiplication computation for one of the PIR servers can be split up over a number of workers (a cluster of workers represents one PIR server). First the database \(D\) needs to be split into parts. It can be done in three ways (see below)
Ways of splitting the database and matrix operation
Fig. 5.2/3
We have one master server that coordinates the workers. When all workers are done
the vector-by-matrix multiplication on their portion of the database, the master respectively adds or concatenates
all of the worker's responses together and sends the result to the requesting client.
Conclusions
According to : 3 :
- The parallelized versions improve the non-parallelized version by approximately a factor of the number of chunks the database is split into.
- The database must be sufficiently large for parallelization of the server-side computation to be beneficial.
Pailier cryptosystem : 8 utilizes the group \(Z^*_{N^2}\), where \(N=pq\) and \(p, q\) are \(n\) bit primes. The construction is as follows:
- KeyGen(\(1^n\)):
- generate \(p, q\) - \(n\) bit primes and compute modulus \(N=pq\) and \(\phi(N) = (p-1)(q-1)\). Modulus \(N\) is the public key and \((N, \phi(N))\) is the private key.
- Encrypt:
- having a public key \(N\) and a message \(m \in Z_N\):
- choose a random \(r \in Z_N^*\)
- compute a ciphertext \(c:= (1+N)^m \cdot r^N \mbox{ mod }N^2\)
- Decrypt:
- having a ciphertext \(c\) and a corresponding private key \((N, \phi(N))\) compute: \[m:= \frac{(c^{\phi(N) \mbox{ mod }N^2}) - 1}{N} \cdot \phi(N)^{-1} \mbox{ mod }N\]
Homomorphic encryption over additive group
\(E(m_1) \cdot E(m_2) = ((1+N)^{m_1} \cdot {r_1}^N \mbox{ mod }N^2) \cdot ((1+N)^{m_2} \cdot {r_2}^N \mbox{ mod }N^2)=\\ (1+N)^{(m_1+m_2) \mbox{ mod } N} \cdot {r_1 r_2}^N \mbox{ mod }N^2 = E(m_1 + m_2 \mbox{ mod }N)\)
Google's MapReduce
As it stays in : 1 it is a programming model for processing and generating large data sets. MapReduce automatically parallelizes and executes the program on a large cluster of commodity machines. The runtime system takes care of the details of partitioning the input data, scheduling the program's execution across a set of machines, handling machine failures, and managing required inter-machine communication. MapReduce allows programmers with no experience with parallel and distributed systems to easily utilize the resources of a large distributed system.
According to : 7 it is perhaps the most widely adopted architecture for scaling parallel computation in public clouds today. Its biggest advantage is that it scales transparently to the programmer. That is, once an implementation is written using MapReduce, it can run on any number of nodes in the data center, from one up to hundreds or thousands, without changes in the code.
As it stays in : 7 MapReduce splits computation into two phases, each of which can be run in parallel on many computing nodes:
- Map phase - the input computation is automatically split equally among available nodes in the cloud data center, and each node is then run a function called map on their respective pieces (called InputSplits). It is important to note that the splitting actually occurs when the data is uploaded into the cloud (in our case when the patient record/files are uploaded) and not when the job is run. This means that each ``mapper'' node will have local access to its InputSplit as soon as computation has started and you avoid a lengthy copying and distributing period. The map function runs a user defined computation on each InputSplit and outputs a number of key-value pairs that go into the next phase
- Reduce phase - takes as input all of the key-value pairs emitted by the mappers and sends them " reducer " nodes in the data center. Specifically, each reducer node receives a single key, along with the sequence of values output by the mappers which share that key. The reducers then take each set and combine it in some way, outputting a single value for each key.
Dean, J., Ghemawat, S.: Mapreduce: a flexible data processing tool.
Commun. ACM 53(1) (2010) 72-77. http://doi.acm.org/10.1145/1629175.1629198
Devet, C., Goldberg, I., Heninger, N.: Optimally robust private information retrieval.
In Kohno, T., ed.: Proceedings of the 21th USENIX Security Symposium, Bellevue, WA, USA, August 8-10, 2012, USENIX Association (2012) 269-283. https://www.usenix.org/conference/usenixsecurity12/technical-sessions/presentation/devet
Devet, C.: Evaluating private information retrieval on the cloud (2013)
Gasarch, W.I.: A survey on private information retrieval (column: Computational complexity).
Bulletin of the EATCS 82 (2004) 72-107. http://theorie.informatik.uni-ulm.de/Personen/toran/beatcs/column82.pdf
Gentry, C.: A fully homomorphic encryption scheme.
Doctoral Thesis, Stanford University (2009)
Goldberg, I.: Improving the robustness of private information retrieval.
In: 2007 IEEE Symposium on Security and Privacy (S&P 2007), 20-23 May 2007, Oakland, California, USA, IEEE Computer Society (2007) 131-148. http://dx.doi.org/10.1109/SP.2007.23
Mayberry, T., Blass, E., Chan, A.H.: PIRMAP: efficient private information retrieval for mapreduce.
IACR Cryptology ePrint Archive 2012 (2012) 398. http://eprint.iacr.org/2012/398
Paillier, P.: Public-key cryptosystems based on composite degree residuosity classes.
In Stern, J., ed.: Advances in Cryptology - EUROCRYPT '99, International Conference on the Theory and Application of Cryptographic Techniques, Prague, Czech Republic, May 2-6, 1999, Proceeding. Volume 1592 of Lecture Notes in Computer Science., Springer (1999) 223-238. http://dx.doi.org/10.1007/3-540-48910-X_16
Smith, K.P., Allen, M.D., Lan, H., Sillers, A.: Making query execution over encrypted data practical.
In Jajodia, S., Kant, K., Samarati, P., Singhal, A., Swarup, V., Wang, C., eds.: Secure Cloud Computing. Springer (2014) 171-188. http://dx.doi.org/10.1007/978-1-4614-9278-8_8
Trostle, J.T., Parrish, A.: Efficient computationally private information retrieval from anonymity or trapdoor groups.
In Burmester, M., Tsudik, G., Magliveras, S.S., Ilic, I., eds.: Information Security - 13th International Conference, ISC 2010, Boca Raton, FL, USA, October 25-28, 2010, Revised Selected Papers. Volume 6531 of Lecture Notes in Computer Science., Springer (2010) 114-128. http://dx.doi.org/10.1007/978-3-642-18178-8_10
Zhang, Y., Juels, A., Reiter, M.K., Ristenpart, T.: Cross-vm side channels and their use to extract private keys.
In Yu, T., Danezis, G., Gligor, V.D., eds.: the ACM Conference on Computer and Communications Security, CCS'12, Raleigh, NC, USA, October 16-18, 2012, ACM (2012) 305-316. http://doi.acm.org/10.1145/2382196.2382230