Zadanie 1.1.2.3
Rysunek
Polecenie
Wybierz pierwszy z poniższych przycisków, aby zobaczyć rozwiązanie wykonane w 3 krokach lub drugi (Odpowiedź), jeśli chcesz sprawdzić wynik.
Polecenie
Prawidłowa odpowiedź odsłoni następny etap rozwiązania.
Pierwszy etap rozwiązywania zadania, metodą wieloboku sznurowego, polega na...(wybierz wśród 3 możliwości)
Stwierdzenie 1 z 3
Krok 1
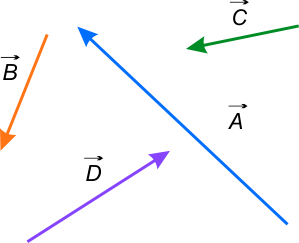
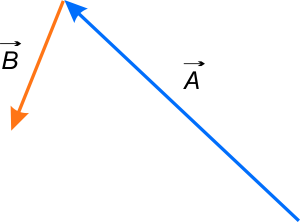
Należy przesunąć wektory w taki sposób, aby dwa ich początki stykały się ze sobą.
Stwierdzenie 2 z 3
Krok 1
Należy przesunąć wektory w taki sposób, aby koniec wektora \(\vec{A}\) stykał się z początkiem wektora \(\vec{B}\).
Stwierdzenie 3 z 3
Krok 1
Należy wszystkie wektory \(\vec{A}\), \(\vec{B}\), \(\vec{C}\) i \(\vec{D}\) przesunąć tak, aby ich końce stykały się.
Na rysunku przedstawiono działanie \(\vec{A}+\vec{B}\).
Dla przypomnienia: należy wykonać działanie \(\left [ \left ( \vec{A}+\vec{B} \right )-\vec{C} \right ]-\vec{D}\) na wektorach.
Polecenie
Drugi etap rozwiązywania zadania polega na...(wybierz wśród 3 możliwości).
Stwierdzenie 1 z 3
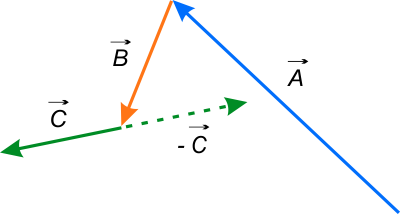
Do końca wektora \(\vec{B}\), należy przesunąć początek wektora \(\vec{C}\), a następnie wyznaczyć wektor przeciwny do wektora \(C\).
Stwierdzenie 2 z 3
Należy wektor \(\vec{C}\) przesunąć do końca wektora \(\vec{A}\).
Stwierdzenie 3 z 3
Należy ustawić tak trzy wektory \(\vec{A}\), \(\vec{B}\), \(\vec{C}\), aby ich początki były w jednym miejscu.
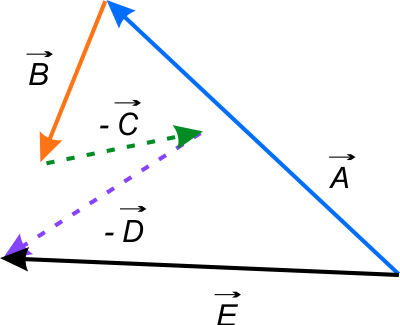
Na rysunku 2 przedstawiono w sposób graficzny działanie \((\vec{A}+\vec{B})-\vec{C}\) w postaci \(\vec{A}+\vec{B}+(-\vec{C}\)).
Polecenie
Trzeci etap rozwiązywania zadania polega na... (wybierz wśród 3 możliwości)
Stwierdzenie 1 z 3
Najdłuższy wektor jest rozwiązaniem zadania.
Stwierdzenie 2 z 3
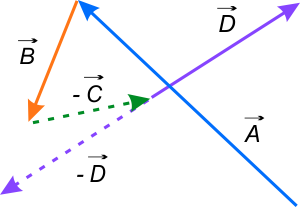
Do końca wektora \(-\vec{C}\), należy przesunąć początek wektora \(-\vec{D}\).
Stwierdzenie 3 z 3
Do początku wektora \((\vec{A}+\vec{B})-\vec{C}\), należy przesunąć koniec wektora \(\vec{D}\).
Na rysunku 3 przedstawiono działanie \(\left [ \left ( \vec{A}+\vec{B} \right )-\vec{C} \right ]-\vec{D}\) w postaci \(\vec{A}+\vec{B}+(-\vec{C})+(-\vec{D})\).
Na koniec wystarczy narysować wektor, którego początek pokrywa się z początkiem wektora \(\vec{A}\), a kończy się na grocie wektora \(-\vec{D}\).