Zadanie 1.2.1.5
  1. Kurs obliczeniowy z fizyki
  2. 1. Wektory
  3. 1.2 Wektory w układzie kartezjańskim
  4. 1.2.1 Nauka
  5. Zadanie 1.2.1.5

 Zadanie 1.2.1.5

Cosinusy kierunkowe
Wektor \(\vec{a}\) tworzy z osiami \(OX\) i \(OY\) kąty równe odpowiednio \(45^{\circ}\) i \( 120^{\circ}\). Wyznacz jego współrzędne. Długość wektora wynosi \(2\).

 Wskazówka teoretyczna

 Teoria – cosinusy kierunkowe
Cosinusy kierunkowe opisują położenie wektora w przestrzeni.

Jeżeli wektor o współrzędnych \(\vec{a}=\left [ a_{x}\,,\,a_{y}\,,\,a_{z} \right ]\) i długości \(\left | \vec{a} \right |\) tworzy odpowiednio z osiami kąty \(\varphi_{x}\, ,\varphi_{y}\, ,\varphi_{z}\), to cosinusy kierunkowe wektora \(\vec{a}\) wynoszą:
\(\displaystyle{cos\,\varphi_{x}=\frac{a_{x}}{\left | \vec{a} \right |}}\),  \(\displaystyle{cos\,\varphi_{y}=\frac{a_{y}}{\left | \vec{a} \right |}}\),  \(\displaystyle{cos\,\varphi_{z}=\frac{a_{z}}{\left | \vec{a} \right |}}\).
Kwadraty cosinusów kierunkowych danego wektora sumują się do jedności:
\(cos^{2}\varphi_{x}+cos^{2}\varphi_{y}+cos^{2}\varphi_{z}=1\)
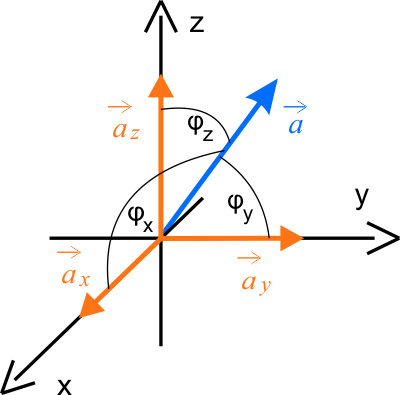
Cosinusy kierunkowe

Dane i szukane

Dane:
- kąt kierunkowy z osią x \(\varphi_{x}=45^{\circ}\),
- kąt kierunkowy z osią y \(\varphi_{y}=120^{\circ}\),
- długość wektora \(\vec{a}=2\).

Szukane:
- współrzędne wektora \(\vec{a}\).

Rozwiązanie

Z definicji cosinusów kierunkowych można zapisać:

\(a_{x}=\left | \vec{a} \right |\cos\,\varphi_{x}\)

Po podstawieniu danych otrzymujemy:

\(\displaystyle{a_{x}=2\cdot \cos\,45^{\circ}=2\cdot \frac{\sqrt{2}}{2}=\sqrt{2}}\)

Podobnie postępujemy w przypadku składowej y-owej:

\(\displaystyle{a_{y}=2\cdot \cos\,120^{\circ}}\)  \(\cos\,120^{\circ}=\cos\,(180^{\circ}-60^{\circ})=-\cos\,60^{\circ}\)  \(\displaystyle{=2\cdot(-\frac{1}{2})=-1 }\)

Do obliczenia została składowa \(a_{z}\). Można policzyć ją korzystając ze wzoru na długość wektora:
 \(\sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}\)  \(2=\sqrt{(\sqrt{2})^{2}+(-1)^{2}+a_{z}^{2}}\) podnosząc obie strony do kwadratu otrzymujemy:

\(4=2+1+ a_{z}^{2}\)
\(a_{z}^{2}=1\)
\( a_{z}= \pm1\)

Odpowiedź

Współrzędne wektora \(\vec{a}\) wynoszą: \( \vec{a}=\left [ \sqrt{2},\,-1,\,1 \right ]=\sqrt{2}\,\hat{i}-\hat{j}+\hat{k}\) lub \( \vec{a}=\left [ \sqrt{2},\,-1,\,-1 \right ]=\sqrt{2}\,\hat{i}-\hat{j}-\hat{k}\).