Zadanie 1.4.1.5
Wskazówka teoretyczna
\[\vec{M}=\vec{R}\times\vec{F}\]
Dane:
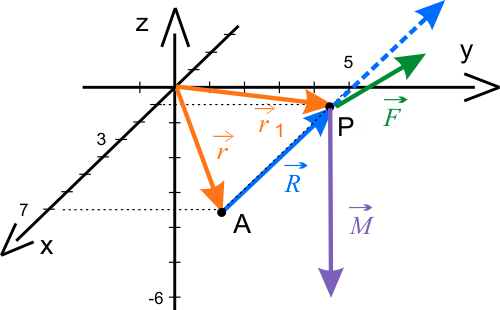
- wektor siły: \(\vec{F}= -3\, \hat{i}+\hat{j}\,\mathrm{[N]}\),
- wektor położenia punktu materialnego: \(\vec{r}= 7\,\hat{i}+5\,\hat{j}\,\mathrm{[m]}\),
- wektor położenia punktu \(P\): \(\vec{r_{1}}= \hat{i}+5\,\hat{j}\,\mathrm{[m]}\).
Szukane:
- moment siły względem punktu \(P\): \(\vec{M}\)
Wektor wodzący jest to wektor łączący początek układu współrzędnych z miejscem w przestrzeni, w którym znajduje się punkt materialny w danej chwili czasu (na rysunku \(\vec{r_{1}}\) oraz \(\vec{r_{2}}\)).
Wektorem położenia punktu B względem punktu A jest wektor wodzący \(\vec{r_{12}}\), którego początek znajduje się w punkcie odniesienia (A), a koniec w punkcie, którego położenie określamy (B).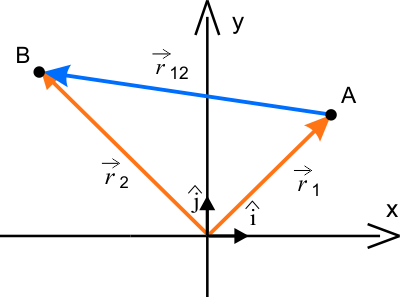
Rozwiązanie
Obliczenia należy rozpocząć od wyznaczenia wektora wodzącego \(\vec{R}\):
\(\vec{R}=\vec{r_1}-\vec{r}=(\hat{i}+5\,\hat{j})-(7\, \hat{i}+5\,\hat{j}) \)
\(\vec{R}=(1-7)\, \hat{i}-(-5+5)\hat{j}=-6\, \hat{i}\)
\(\vec{R}=-6\, \hat{i}\,\mathrm{[m]}\)
Moment tej siły względem punktu \(P\) jest iloczynem wektorowym \(\vec{M}=\vec{R}\times\vec{F}\):
\(\vec{M}=(R_{y}F_{z}-F_{y}R_{z})\, \hat{i}+(R_{z}F_{x}-F_{z}R_{x})\,\hat{j}+(R_{x}F_{y}-F_{x}R_{y})\, \hat{k}\)
\(\vec{M}=(0\cdot 0-1\cdot 0)\, \hat{i}+(0\cdot(-3)-0\cdot(-6))\,\hat{j}+(-6\cdot1-(-3)\cdot0)\, \hat{k}\)
\(\vec{M}=0\, \hat{i}+0\,\hat{j}-6\, \hat{k}=-6\, \hat{k}\,\mathrm{[m\cdot N]}\)
Wektor momentu siły ma różną od zera jedynie składową zetową, czyli jest prostopadły do płaszczyzny \(XY\).
Odpoweidź
Moment siły wynosi \(\vec{M}=-6\, \hat{k}\,\mathrm{[m\cdot N]}\).