Analiza sytuacji

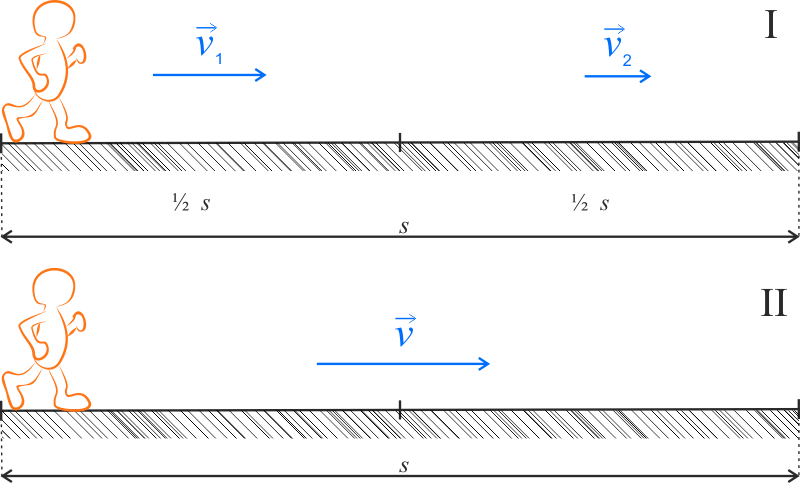
Na rysunku rzymską liczbą \(\mathrm{I}\) oznaczono podstawową wersję biegu, w której każda połowa trasy jest pokonywana z inną szybkością, natomiast liczbą \(\mathrm{II}\) oznaczono wersję alternatywną biegu z jedną, stałą szybkością.

Można zauważyć, że zadanie należy rozwiązać przez porównanie dwóch wariantów biegu. O pierwszym wariancie biegu wiadomo zbyt mało, zatem należy zastanowić się więc nad wariantem drugim, w którym podana jest wartość szybkość biegu \(v\). Szybkość ta jest stała na całej długości trasy \(s\), czyli można przyjąć, że jest ona zgodna z definicją szybkości średniej.

Rozwiązanie

Czas przebycia pierwszej połowy trasy wynosi:  \(\displaystyle{t_1=\frac{\Large{\frac{S}{2}}}{v_1}}=\frac{S}{2v_1}\)

Analogicznie czas przebycia drugiej połowy trasy wynosi:  \(\displaystyle{t_2=\frac{S}{2v_2}}\)

Czas przebycia całej trasy wynosi: 

Gdyby biegacz biegł cały czas z szybkością \(v\), to czas przebycia całej trasy byłby taki sam, czyli:
Porównując obie strony powyższych równań mamy:
Po obustronnym pomnożeniu przez \(\displaystyle{\frac{2}{S}}\)  mamy:

Obliczenia

\(\displaystyle{v_2=\frac{v_1v}{2v_1-v}}=\frac{18\cdot 12}{2\cdot18-12}=9\,\mathrm{\frac{km}{h}}\)