Zadanie 2.1.2.2
  1. Kurs obliczeniowy z fizyki
  2. 2. Kinematyka
  3. 2.1. Ruch prostoliniowy
  4. 2.1.2 Trening
  5. Zadanie 2.1.2.2

Zadanie 2.1.2.2

Składanie prędkości
Prędkość łodzi względem wody w spoczynku wynosi \(\vec{v}_1\). Woda płynie w rzece z prędkością \(\vec{v}_2\). Jak należy skierować łódź, aby przepłynąć rzekę w kierunku prostopadłym do brzegu? W jakim czasie łódź przepłynie rzekę o szerokości \(d\)? Przedstaw graficznie układ prędkości. Obliczenia numeryczne wykonaj dla \(\displaystyle{v_1=5\,\mathrm{\frac{m}{s}}}\),  \(\displaystyle{v_2=3\,\mathrm{\frac{m}{s}}}\),  \(d=80\,\mathrm{m}\).

Informacja

Możesz zobaczyć odpowiedź, klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- szybkość łodzi względem rzeki \(\displaystyle{v_1=5\,\mathrm{\frac{m}{s}}}\),
- szybkość wody w rzece \(\displaystyle{v_2=3\,\mathrm{\frac{m}{s}}}\),
- szerokość rzeki \(d=80\,\mathrm{m}\).

Dane:
- czas przepływania rzeki \(t\),
- kąt, pod jakim należy skierować łódź, aby przepłynęła ona prosto na drugi brzeg \(\alpha\).

Odpowiedź

Łódź należy skierować pod prąd rzeki, pod kątem \(\alpha\approx37^{\circ}\), w kierunku prostopadłym do jej brzegów. Wówczas łódź przepłynie rzekę w ciągu \(20\, \mathrm{s}\).

Polecenie

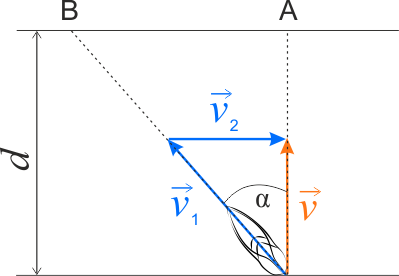
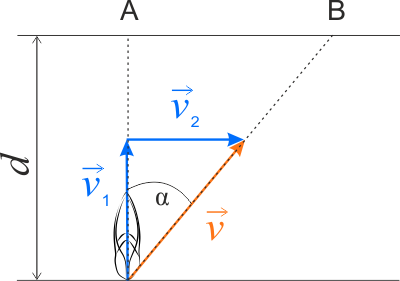
Z przedstawionych poniżej dwóch rysunków wybierz ten, który ilustruje jak należy skierować łódź, aby przepłynąć rzekę w kierunku prostopadłym do brzegu.

Rysunek 1


\(\vec{v}_2\) - prędkość wody w rzece,
\(\vec{v}_1\) - prędkość łodzi względem rzeki,
\(\vec{v}\) - prędkość wypadkowa łodzi.

Odpowiedź prawidłowa

Rysunek 1


\(\vec{v}_2\) - prędkość wody w rzece,
\(\vec{v}_1\) - prędkość łodzi względem rzeki,
\(\vec{v}\) - prędkość wypadkowa łodzi.

Odpowiedź nieprawidłowa
Jeżeli łódź zostanie skierowana prostopadle do brzegu, wtedy prąd rzeki zniesie ją tak, że przybije do przeciwległego brzegu w punkcie \(B'\). Aby łódź wylądowała w punkcie \(A\), należy skierować ją tak, by wypadkowa prędkości \(\vec{v}\) była prostopadła do brzegów.

Polecenie

Wskaż prawidłową wartość kąta \(\alpha\) wśród czterech podanych poniżej.

Wzór 1 z 4

\(\alpha=37^{\circ}\)

Odpowiedź prawidłowa

Wzór 2 z 4

\(\alpha=32^{\circ}\)

Odpowiedź nieprawidłowa

Wzór 3 z 4

\(\alpha=41^{\circ}\)

Odpowiedź nieprawidłowa

Wzór 4 z 4

\(\alpha=30^{\circ}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Rysunek

Na rysunku widać, że kąt pomiędzy prostopadłą do brzegów, a kierunkiem wypłynięcia łodzi musi spełniać warunek:
\(\displaystyle{\sin{\alpha}=\frac{v_2}{v_1}=\frac{3}{5}=0,6}\)
\(\alpha\approx37^{\circ}\)

Polecenie

Wskaż jeden z dwóch zestawów zależności, z których należy skorzystać podczas obliczeń w drugiej części zadania.

Wybór 1 z 2

\(\displaystyle{v=\frac{d}{t}}\)   oraz    \(v=\sqrt{v_{1}^{2}+v_{2}^{2}}\)

Odpowiedź nieprawidłowa

Wybór 2 z 2

\(\displaystyle{v=\frac{d}{t}}\)   oraz    \(v=\sqrt{v_{1}^{2}-v_{2}^{2}}\)

Odpowiedź prawidłowa

Rozwiązanie

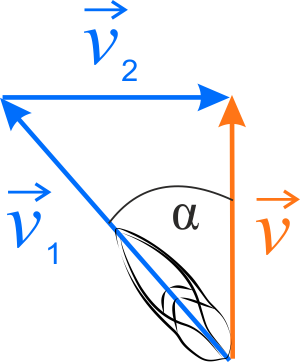
Prędkość wypadkowa łodzi względem brzegów rzeki wynosi \(\vec{v}_1=\vec{v}+\vec{v}_2\). Wektory te tworzą trójkąt prostokątny, więc do wyznaczenia wartości prędkości czyli szybkości wypadkowej łodzi można użyć twierdzenie Pitagorasa.

\(v_1^2=v^2+v_2^2\)
\(v^2=v^2_1-v_2^2\)
\(v=\sqrt{v_1^2-v_2^2}\)
Łódź porusza się ruchem jednostajnym, więc czas ruchu należy wyznaczyć z zależności \(\displaystyle{v=\frac{d}{t}}\).

Polecenie

Wskaż, jedną wśród czterech, prawidłową wartość czasu, w którym łódź przepłynie rzekę.

Wybór 1 z 4

\(t=10\,\mathrm s\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(t=15\,\mathrm s\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(t=20\,\mathrm s\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(t=25\,\mathrm s\)

Odpowiedź nieprawidłowa

Rozwiązanie

Obliczenia czasu przepłynięcia rzeki, wymaga skorzystania z układu równań:

\(\begin{cases} v =\sqrt{v_1^2-v_2^2}\\ \displaystyle{v=\frac{d}{t}} \end{cases}\)

\(\displaystyle{\sqrt{v_1^2-v_2^2}=\frac{d}{t}}\)

\(\displaystyle{t=\frac{d}{\sqrt{v_1^2-v_2^2}}}\)    \(\begin{bmatrix} \displaystyle{\mathrm{\frac{m}{\large{\sqrt{\frac{m^2}{s^2}}}}=\frac{m}{\large{\frac{m}{s}}}=s}} \end{bmatrix}\)

\(\displaystyle{t=\frac{80}{\sqrt{5^2-3^2}}=\frac{80}{4}=20\,\mathrm{s}}\)

Odpowiedź

Łódź należy skierować pod prąd rzeki, pod kątem \(\alpha\approx37^{\circ}\), w kierunku prostopadłym do jej brzegów. Wówczas łódź przepłynie rzekę w ciągu \(20\, \mathrm{s}\).