Zadanie 2.1.2.3
  1. Kurs obliczeniowy z fizyki
  2. 2. Kinematyka
  3. 2.1. Ruch prostoliniowy
  4. 2.1.2 Trening
  5. Zadanie 2.1.2.3

 Zadanie 2.1.2.3

Ruch prostoliniowy jednostajnie zmienny
Określ czas wznoszenia się windy, zakładając, że jej ruch podczas ruszania i hamowania jest jednostajnie zmienny o przyspieszeniu równym, co do wartości bezwzględnej \(\displaystyle{a=1\, \mathrm{\frac{m}{s^2}}}\), a na środkowym odcinku drogi, ruch jest jednostajny z szybkością \(\displaystyle{v=2\, \mathrm{\frac{m}{s}}}\). Wysokość, na którą wznosi się winda to \(h=60\, \mathrm{m}\). Sporządź wykres prędkości windy od czasu trwania jej ruchu.

Informacja

Możesz zobaczyć odpowiedź, klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- przyspieszenie podczas ruszania windy: \(\displaystyle{a=1\,\mathrm{\frac{m}{s^2}}}\),
- przyspieszenie podczas hamowania windy: \(\displaystyle{a=-1\,\mathrm{\frac{m}{s^2}}}\),
- prędkość windy na środkowym odcinku: \(\displaystyle{v=2\,\mathrm{\frac{m}{s}}}\),
- wysokość, na którą wznosi się winda: \(h=60\,\mathrm{m}\).

Szukane:
- czas wznoszenia się windy \(t\),
- wykres prędkości windy od czasu trwania jej ruchu.

Odpowiedź

Wykres prędkości windy od czasu trwania jej ruchu
Wykres prędkości windy od czasu trwania jej ruchu.

Czas wznoszenia się windy wynosi \(32\,\mathrm{s}\).

Polecenie

Ruch windy można podzielić na 3 etapy: ruszanie (\(t_1\) oraz \(S_1\)), ruch jednostajny (\(t_2\) oraz \(S_2\)) i hamowanie (\(t_3\) oraz \(S_3\)). Oblicz czas nabierania prędkości przez windę podczas ruszania. Wybierz jedna prawidłową wartość spośród czterech.

Wybór 1 z 4

\(t_1=0,5\,\mathrm{s}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(t_1=1\,\mathrm{s}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(t_1=2\,\mathrm{s}\)

Odpowiedź prawidłowa

Wybór 4 z 4

\(t_1=4\,\mathrm{s}\)

Odpowiedź nieprawidłowa

Rozwiązanie - etap 1 ruszanie

Przy ruszaniu windy jej prędkość wzrasta od wartości \(0\) do \(\displaystyle{2\, \mathrm{\frac{m}{s}}}\) z przyspieszeniem \(\displaystyle{a=1\,\mathrm{\frac{m}{s^2}}}\).
Czas trwania tego ruchu można obliczyć z zależności dla ruchu jednostajnie przyspieszonego:

\(v=v_0+at_1\)

Szybkość początkowa \(v_0=0\)  więc \(v=at_1\)
Po przekształceniu mamy: 
\(\displaystyle{t_1=\frac{v}{a}}=\frac{2}{1}=2\,\mathrm{s}\)   \(\displaystyle{\left [\mathrm{\frac{\frac{m}{s}}{\frac{m}{s^2}}=\frac{m}{s}\cdot\frac{s^2}{m}=s}  \right ]}\)

Czas hamowania windy jest taki sam, ponieważ prędkość maleje o taką samą wartość, z takim samym co do wartości bezwzględnej przyspieszeniem.

Polecenie

Jaką drogę podczas ruszania przebyła winda? Wskaż jedną prawidłową odpowiedź z dwóch.

Winda przyspieszała na odcinku \(2\,\mathrm{m}\), ponieważ

\(\displaystyle{S_1=\frac{a\,t_1^2}{2}=\frac{4}{2}=2\,\mathrm{m}}\)

Odpowiedź prawidłowa

Winda przyspieszała na odcinku \(1\,\mathrm{m}\), ponieważ

\(\displaystyle{S_1=\frac{v}{t_1}=\frac{2}{2}=1\,\mathrm{m}}\)

Odpowiedź nieprawidłowa
Podczas ruszania, winda porusza się ruchem jednostajnie przyspieszonym, więc drogę należy obliczać przy pomocy zależności:
\[S=S_0+v_0t+\frac{1}{2}at^2\]
W naszym przypadku wartość drogi początkowej, jak i szybkości początkowej, wynosi zero.

Polecenie

Wskaż, spośród czterech, jedną prawidłową wartość przebytej drogi, podczas ruchu jednostajnego w górę.

Wybór 1 z 4

\(S_2=54\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(S_2=56\,\mathrm{m}\)

Odpowiedź prawidłowa

 Wybór 3 z 4
 
\(S_2=58\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(S_2=60\,\mathrm{m}\)

Odpowiedź nieprawidłowa

Obliczenia - etap 2

Winda pokonuje ruchem jednostajnym drogę \(S_2\). Wysokość, na którą wznosi się winda wynosi:

\(h=S_1+S_2+S_3\)

Droga hamowania i ruszania jest taka sama, ponieważ prędkość maleje o taką samą wartość z takim samym co do wartości bezwzględnej przyspieszeniem, zatem wyrażenie na drogę można zapisać:
\(S_2=h-S_1-S_3=60-2-2=56\,\mathrm{m}\)

Rozwiązanie - etap 2 ruch jednostajny

W etapie drugim ruchu winda porusza się ruchem jednostajnym. Ruch ten opisuje zależność: \(\displaystyle{v_2=\frac{S_2}{t_2}}\).
Mając daną szybkość oraz drogę w tym ruch w łatwy sposób można wyznaczyć czas:

\(\displaystyle{t_2=\frac{S_2}{v_2}=\frac{56}{2}=28\,\mathrm{s}}\)  \(\displaystyle{\left [\mathrm{\frac{m}{\frac{m}{s}}=m\cdot\frac{s}{m}=s} \right ]}\)

Czas wznoszenia się windy wynosi  \(t=t_1+t_2+t_3=2+28+2=32\,\mathrm{s}\)

Polecenie

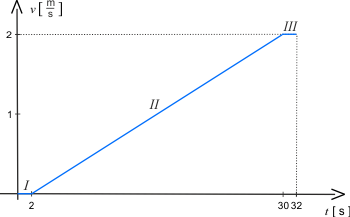
Wskaż jeden wykres, wśród dwóch, który przedstawia sytuacje z zadania.

Wykres 1

Rysunek

Odpowiedź prawidłowa

Wykres 2

Rysunek

Odpowiedź nieprawidłowa
Na wykresie 1 widzimy trzy etapy ruchu:
I   - ruch jednostajnie przyspieszony,
II  - ruch jednostajny,
III - ruch jednostajnie opóźniony.

Odpowiedź

Czas wznoszenia się windy wynosi \(32\,\mathrm{s}\).