Zadanie 2.1.2.4
  1. Kurs obliczeniowy z fizyki
  2. 2. Kinematyka
  3. 2.1. Ruch prostoliniowy
  4. 2.1.2 Trening
  5. Zadanie 2.1.2.4

 Zadanie 2.1.2.4

Ruch jednostajnie zmienny
Dwa pojazdy jechały jednakowo długo. Pierwszy z nich połowę czasu jechał z przyspieszeniem \(a\), a druga połowę z przyspieszeniem \(3a\). Drugi z kolei pierwszą połowę czasu jechał z przyspieszeniem \(2a\), a drugą z przyspieszeniem \(a\). Wyznacz stosunek przebytych dróg przez pojazd \(A\) oraz \(B\). Ile wynoszą te drogi jeśli \(\displaystyle{a=2\,\mathrm{\frac{m}{s^2}}}\), a czas ruchu wynosi: \(t=20\,\mathrm{s}\). Przedstaw tę sytuację na wykresie prędkości w funkcji czasu.

Informacja

Możesz zobaczyć odpowiedź, klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- czas ruchu pojazdów \(t=20\,\mathrm{s}\),
- przyspieszenie \(\displaystyle{a=2\,\mathrm{\frac{m}{s^2}}}\),
- pierwszy etap ruchu pojazdu \(A\):    \(\displaystyle{t_{1A}=\frac{1}{2}t}\),  \(a_{1A}=a\),
- drugi etap ruchu pojazdu \(A\):         \(\displaystyle{t_{2A}=\frac{1}{2}t}\),  \(a_{2A}=3a\),
- pierwszy etap ruchu pojazdu \(B\):    \(\displaystyle{t_{1B}=\frac{1}{2}t}\),  \(a_{1B}=2a\),
- drugi etap ruchu pojazdu \(B\):         \(\displaystyle{t_{2B}=\frac{1}{2}t}\),  \(a_{2B}=a\),

Szukane:
- stosunek dróg przebytych przez pojazd \(A\) oraz \(B\):   \(\displaystyle{\frac{S_B}{S_A}}\),
- wartość drogi przebytej przez pojazd pierwszy \(S_A\),
- wartość drogi przebytej przez pojazd drugi \(S_B\),
- wykres zależności prędkości w funkcji czasu.

Odpowiedź

Stosunek dróg przebytych przez pojazd \(A\) oraz \(B\) wynosi \(\displaystyle{\frac{S_B}{S_A}=\frac{7}{6}}\). Pierwszy pojazd przebył drogę \(S_A=600\, \mathrm{m}\), a drugi \(S_B=700\, \mathrm{m}\).

Wykres prędkości w funkcji czasu

Wykres prędkości w funkcji czasu

Polecenie

Ruch pojazdu \(A\) można podzielić na dwa etapy - w pierwszej i drugiej połowie czasu ruchu. Wyznacz zależność na drogę, jaką przebył pojazd \(A\) w ciągu całego czasu. Wybierz jedna prawidłową wartość spośród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\displaystyle{S_A=\frac{3}{8}at^2}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(\displaystyle{S_A=\frac{3}{4}at^2}\)

Odpowiedź prawidłowa

Wybór 3 z 4

\(\displaystyle{S_A=\frac{1}{4}at^2}\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(\displaystyle{S_A=\frac{1}{2}at^2}\)

Odpowiedź nieprawidłowa

Rozwiązanie - pojazd A

Przebytą drogę pojazdu \(A\) można zapisać następująco:

\(S_A=S_{1A}+S_{2A}\),
gdzie indeksy \(1A\) oraz \(2A\) oznaczają odpowiednio pierwszą i druga połowę czasu.

Pierwszy etap ruchu pojazdu \(A\) - szybkość oraz droga początkowa wynosi zero.

\(\displaystyle{S_{1A}=\frac{a_{1A}\,t_{1A}^2}{2}=\frac{a\,(\frac{t}{2})^2}{2}=\frac{at^2}{8}}\)

Drugi etap ruchu pojazdu \(A\):

\(\displaystyle{S_{2A}=v_A\,t_{2A}+\frac{a_{2A}\,t_{2A}^2}{2}=v_A\,\frac{t}{2}+\frac{3a\,(\frac{t}{2})^2}{2}}\)
\(\displaystyle{S_{2A}=\frac{1}{2}v_A\,t+\frac{3a\,t^2}{8}}\)

\(v_A\) jest szybkością jaką osiągną pojazd \(A\) po połowie czasu. Szybkość ta wynosi:

\(\displaystyle{v_A=a_{1A}\,t_{1A}=a\,\frac{t}{2}=\frac{1}{2}a\,t}\)

Droga w drugim etapie ruchu wynosi:

\(\displaystyle{S_{2A}=\frac{1}{2}v_A\,t+\frac{3a\,t^2}{8}=\frac{1}{2}\cdot\frac{1}{2}at\cdot\,t+\frac{3a\,t^2}{8}}\)
\(\displaystyle{S_{2A}=\frac{2\cdot at^2}{2\cdot 4}+\frac{3a\,t^2}{8}=\frac{5a\,t^2}{8}}\)
Droga przebyta przez pojazd \(A\) wynosi:

\(\displaystyle{S_A=S_{1A}+S_{2A}=\frac{at^2}{8}+\frac{5a\,t^2}{8}=\frac{6a\,t^2}{8}}\)
\(\displaystyle{S_A=\frac{3}{4}at^2}\)

Rozwiązanie

Wartość drogi przebytej przez pojazd \(A\) wynosi:

\(\displaystyle{S_A=\frac{3}{4}at^2=\frac{3}{4}\cdot 2\cdot 20^2=600\,\mathrm{m}}\)   \(\left [\displaystyle{\mathrm{ \frac{m}{s^2}\cdot s^2=m }}\right ]\)

Polecenie

Ruch pojazdu \(B\) można podzielić na dwa etapy - ruch w pierwszej i drugiej połowie czasu ruchu. Wyznacz zależność na drogę, jaką przebył pojazd \(B\) w ciągu całego czasu. Wybierz jedną prawidłową wartość, spośród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\displaystyle{S_B=\frac{7}{8}at^2}\)

Odpowiedź prawidłowa

Wybór 2 z 4

\(\displaystyle{S_B=\frac{5}{8}at^2}\)

Odpowiedź nieprawidłowa

Wybór 3 z 4

\(\displaystyle{S_B=\frac{3}{4}at^2}\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(\displaystyle{S_B=\frac{1}{4}at^2}\)

Odpowiedź nieprawidłowa

Rozwiązanie - pojazd B

Przebytą drogę pojazdu \(B\) można zapisać następująco:

\(S_B=S_{1B}+S_{2B}\),
gdzie indeksy \(1B\) oraz \(2B\) oznaczają odpowiednio pierwszą i druga połowę czasu.

Pierwszy etap ruchu pojazdu \(B\) - szybkość oraz droga początkowa wynosi zero.

\(\displaystyle{S_{1B}=\frac{a_{1B}\,t_{1B}^2}{2}=\frac{2a\,(\frac{t}{2})^2}{2}=\frac{at^2}{4}}\)

Drugi etap ruchu pojazdu \(B\)

\(\displaystyle{S_{2B}=v_B\,t_{2B}+\frac{a_{2B}\,t_{2B}^2}{2}=v_B\,\frac{t}{2}+\frac{a\,(\frac{t}{2})^2}{2}}\)
\(\displaystyle{S_{2B}=\frac{1}{2}v_B\,t+\frac{a\,t^2}{8}}\)

\(v_B\) jest szybkością jaką osiągną pojazd \(B\) po połowie czasu. Szybkość ta wynosi:

\(\displaystyle{v_B=a_{1B}\,t_{1B}=2a\,\frac{t}{2}=a\,t}\)

Droga w drugim etapie ruchu wynosi:

\(\displaystyle{S_{2B}=\frac{1}{2}v_B\,t+\frac{a\,t^2}{8}=\frac{1}{2}\cdot at\cdot\,t+\frac{a\,t^2}{8}}\)
\(\displaystyle{S_{2B}=\frac{4at^2}{8}+\frac{a\,t^2}{8}=\frac{5a\,t^2}{8}}\)

Droga przebyta przez pojazd \(B\) wynosi:
\(\displaystyle{S_B=S_{1B}+S_{2B}=\frac{at^2}{4}+\frac{5a\,t^2}{8}}\)
\(\displaystyle{S_B=\frac{7}{8}at^2}\)

Rozwiązanie

Wartość drogi przebytej przez pojazd \(B\) wynosi:

\(\displaystyle{S_B=\frac{7}{8}at^2=\frac{7}{8}\cdot 2\cdot 20^2=700\,\mathrm{m}}\) \(\left [\displaystyle{\mathrm{ \frac{m}{s^2}\cdot s^2=m }}\right ]\)

Polecenie

Wskaż, spośród dwóch, jeden prawidłowy zestaw szybkości pojazdów w połowie czasu ruchu \(v_A\), \(v_B\) oraz ich szybkości końcowe \(v_{KA}\), \(v_{KB}\).

Zestaw 1 z 2

\(\displaystyle{v_A=20\,\mathrm {\frac{m}{s}}}\)
\(\displaystyle{v_B=40\,\mathrm {\frac{m}{s}}}\)
\(\displaystyle{v_{KA}=80\,\mathrm {\frac{m}{s}}}\)
\(\displaystyle{v_{KB}=60\,\mathrm {\frac{m}{s}}}\)

Odpowiedź prawidłowa

Zestaw 2 z 2

\(\displaystyle{v_A=10\,\mathrm {\frac{m}{s}}}\)
\(\displaystyle{v_B=20\,\mathrm {\frac{m}{s}}}\)
\(\displaystyle{v_{KA}=40\,\mathrm{ \frac{m}{s}}}\)
\(\displaystyle{v_{KB}=30\,\mathrm{ \frac{m}{s}}}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Szybkości pojazdów w połowie czasu ruchu zostały policzone powyżej i wynoszą:

\(\displaystyle{v_A=\frac{1}{2}at=\frac{1}{2}\cdot 2\cdot20=20\,\mathrm {\frac{m}{s}}}\)  \(\left [\displaystyle{\mathrm{ \frac{m}{s^2}\cdot s^2=m }}\right ]\)
\(\displaystyle{v_B=at=2\cdot20=40\,\mathrm {\frac{m}{s}}}\)

Szybkość końcowa pojazdu \(A\) wynosi:
\(\displaystyle{v_{KA}=v_A+3a\frac{t}{2}=\frac{1}{2}at+\frac{3}{2}at=2at}\)
\(\displaystyle{v_{KA}=2at=2\cdot 2\cdot20=80\,\mathrm {\frac{m}{s}}}\)

Szybkość końcowa pojazdu \(B\) wynosi:
\(\displaystyle{v_{KB}=v_B+a\frac{t}{2}=at+\frac{1}{2}at=\frac{3}{2}at}\)
\(\displaystyle{v_{KB}=\frac{3}{2}at=\frac{3}{2}\cdot 2\cdot20=60\,\mathrm {\frac{m}{s}}}\)

Polecenie

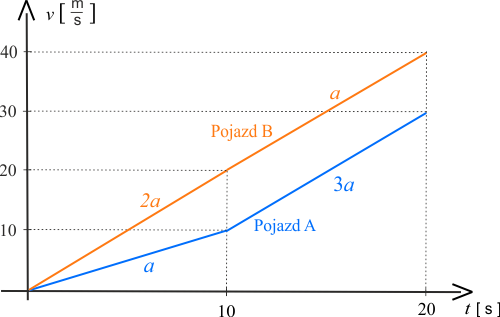
Wybierz, z dwóch poniższych, jeden prawidłowy wykres prędkości w funkcji czasu dwóch pojazdów.

Wybór 1 z 2
Wykresie prędkości w funkcji czasu

Odpowiedź nieprawidłowa

Wybór 2 z 2
Wykresie prędkości w funkcji czasu

Odpowiedź prawidłowa

Odpowiedź

Stosunek dróg przebytych przez pojazd \(A\) oraz \(B\) wynosi \(\displaystyle{\frac{S_B}{S_A}=\frac{7}{6}}\). Pierwszy pojazd przebył drogę \(S_A=600\, \mathrm{m}\), a drugi \(S_B=700\, \mathrm{m}\).

Wykres wartości prędkości w funkcji czasu

Wykres prędkości w funkcji czasu