Zadanie 2.2.1.1

Prędkość średnia

Położenie ciała w chwili początkowej wyznaczał wektor wodzący

$\vec{r}_1=2\,\hat{i}-3\,\hat{j}\, \mathrm{[m]}$ . Po

$5$ sekundach nowe położenie ciała określał wektor

$\vec{r}_2=3\,\hat{i}+4\,\hat{j}\,\mathrm{[m]}$ . Wyznacz wektor prędkości średniej przemieszczania się ciała.

Wskazówka teoretyczna

Teoria - prędkość średnia

Zgodnie z definicją, prędkość średnia wynosi

$\displaystyle{\vec{v}_{sr}=\frac{\bigtriangleup \vec{r}}{\bigtriangleup t}}$ ,
gdzie:

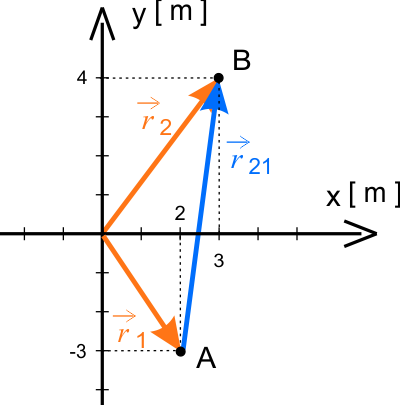
$\bigtriangleup \vec{r}=\vec{r}_2-\vec{r}_1$ - wektor wodzący,

$\bigtriangleup t$ - przedział czasu.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- wektor pierwszy o współrzędnych $\vec{r_{1}}=2\,\hat{i}-3\,\hat{j}$ [m],
- wektor drugi o współrzędnych $\vec{r_{2}}=3\,\hat{i}+4\,\hat{j}$ [m].

Szukane:
- współrzędne wektora prędkości średniej.

Wektory wodzące w układzie współrzędnych

Rozwiązanie

Wektor średniej prędkość przemieszczania wynosi:

$\displaystyle{\vec{v}_{śr}=\frac{\bigtriangleup \vec{r}}{\bigtriangleup t}=\frac{\vec{r_2}-\vec{r_1}}{t_2-t_1}}$

$\displaystyle{\vec{v}_{śr}=\frac{(3\,\hat{i}+4\,\hat{j})-(2\,\hat{i}-3\,\hat{j})}{5}=\frac{\hat{i}+7\,\hat{j}}{5}=\frac{1}{5}\,\hat{i}+\frac{7}{5}\,\hat{j} \;\mathrm{\begin{bmatrix}\large{\frac{m}{s}} \end{bmatrix}}}$

Odpowiedź

Wektor prędkości średniej przemieszczania ciała wynosi $\displaystyle{\vec{v}_{śr}=\frac{1}{5}\,\hat{i}+\frac{7}{5}\,\hat{j}\;\begin{bmatrix}\mathrm{\large{\frac{m}{s}}} \end{bmatrix}}$ .

Wstęp

1. Wektory

2. Kinematyka

3. Zasady dynamiki

4. Praca, moc, energia, pęd

5. Dynamika układu punktów

6. Drgania i fale

7. Elektryczność

Ankieta