Zadanie 2.2.1.2
  1. Kurs obliczeniowy z fizyki
  2. 2. Kinematyka
  3. 2.2. Ruch w układzie kartezjańskim
  4. 2.2.1 Nauka
  5. Zadanie 2.2.1.2

 Zadanie 2.2.1.2

Poruszające sie cząstki w układzie kartezjańskim
Cząstki \(A\) i \(B\) poruszają się wzdłuż osi współrzędnych kartezjańskiego układu odniesienia. Cząstka \(A\) z prędkością \(\displaystyle{\vec{v}_A =2\hat{i}\;\mathrm{\frac{km}{s}}}\) wzdłuż osi \(x\), a cząstka \(B\) wzdłuż osi \(y\) z prędkością \(\displaystyle{\vec{v}_B =4\hat{j}\;\mathrm{\frac{km}{s}}}\). W chwili \(t=0\,\mathrm{s}\) cząstka \(A\) znajduje się w punkcie o współrzędnych \(P_A=(-5,0)\;\mathrm{km}\), natomiast cząstka \(B\) w punkcie o współrzędnych \(P_B=(0,-5)\;\mathrm{km}\). Określ zależność od czasu wektora położenia cząstki \(B\) względem \(A\). W którym miejscu oraz w jakim momencie czasu, cząstki będą najbliżej siebie?

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- prędkość cząstki \(A\): \(\displaystyle{\vec{v}_A =2\hat{i}\;\mathrm{\frac{km}{s}}}\),
- prędkość cząstki \(B\): \(\displaystyle{\vec{v}_B =4\hat{j}\;\mathrm{\frac{km}{s}}}\),
- położenie cząstki \(A\) w chwili \(t=0\): \(P_A=(-5,0)\;\mathrm{km}\),
- położenie cząstki \(B\) w chwili \(t=0\): \(P_B=(0,-5)\;\mathrm{km}\).

Szukane:
- wektor położenia cząstki \(B\) względem \(A\),
- czas, w którym cząstki będą najbliżej siebie,
- położenie cząstek, w momencie kiedy odległość między nimi będzie najmniejsza.

Rozwiązanie

Położenia cząstek można narysować w kartezjańskim układzie odniesienia. Na poniższym rysunku pokazane są położenia cząstek w chwili \(t = 0\) jak i odpowiadające im wektory położenia oraz prędkości.

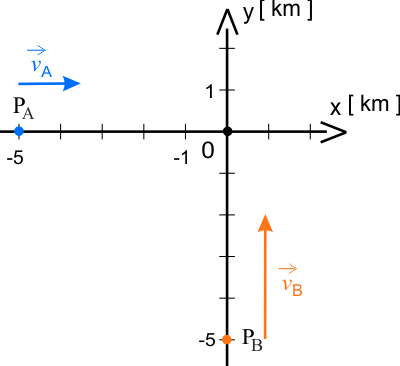
Wykres położenia cząstek w chwili \(t=0\)

Wykres położenia cząstek w chwili \(t=0\)

Wektory wodzące cząstek w chwili początkowej wynoszą:
\(\vec{r}_{Ao}=-5\,\hat{i}+0\,\hat{j}=-5\,\hat{i}\;\mathrm{km}\)
\(\vec{r}_{Bo}=0\,\hat{i}-5\,\hat{j}=-5\,\hat{j}\;\mathrm{km}\)

Wektor położenia cząstki \(B\) względem \(A\) obliczamy odejmując wektor położenia jednej cząstki od drugiej:
\(\vec{r}_{B}-\vec{r}_{A}=(5\hat{i}-5\hat{j})\)

Drogę przebytą przez ciało w ruchu jednostajnym można zapisać jako:
\(\vec{r}(t)=\vec{r}_o+\vec{v}\cdot t\)

Dla sytuacji z zadania mamy: \(\vec{r}_A(t)=\vec{r}_{Ao}+\vec{v}_A\cdot t\)  oraz  \(\vec{r}_B(t)=\vec{r}_{Bo}+\vec{v}_B\cdot t\). Podstawiając dane z zadania otrzymujemy:
\(\vec{r}_A(t)=-5\,\hat{i}+2\,\hat{i}t=(-5+2t)\,\hat{i}\)
\(\vec{r}_B(t)=-5\,\hat{j}+4\,\hat{j}t=(-5+4t)\,\hat{j}\)

Wektor położenia cząstki \(B\) względem \(A\) w funkcji czasu wynosi:
\(\vec{r}_B-\vec{r}_A=\left [ (-5+4t)\,\hat{j}-(-5+2t)\,\hat{i} \right ]\)
\(\vec{r}_B-\vec{r}_A=\left [(5-2t)\hat{i}+(-5+4t)\hat{j} \right ]\;\mathrm{km}\)

Odległość między cząstkami wynosi:
\(d=\left | \vec{r}_B-\vec{r}_A \right |=\sqrt{(5-2t)^2+(-5+4t)^2}\;\mathrm{km}\)
\(d=\sqrt{25-20t+4t^2+25-40t+16t^2}\;\mathrm{km}\)
\(d=\sqrt{20t^2-60t+50}\;\mathrm{km}\)

W zadaniu należy sprawdzić kiedy cząstki znajdują się najbliżej siebie. Powyżej została wyznaczona funkcja określająca względne położenie cząstek. Odległość między cząstkami jest najmniejsza, gdy funkcja \(d(t)\) przyjmuje minimalną wartość lub też funkcja  \(f(t)=20t^2-60t+50\) osiąga minimum.

Funkcja \(f(t)\) jest parabolą skierowaną ramionami „do góry”. Położenie wierzchołka (minimum) tej paraboli możemy wyznaczyć na podstawie własności trójmianu kwadratowego.  \(\displaystyle{t=p=-\frac{b}{2a}=-\frac{-60}{2\cdot20}=\frac{3}{2}}\)  Można również obliczyć pochodną tej funkcji i sprawdzić dla jakiego \(t\) pochodna ta przyjmuje wartość zero.

\(\displaystyle{\frac{\mathrm{d} f(t)}{\mathrm{d} t}=20\cdot 2t-60}\)
\(40t-60=0\)
\(\displaystyle{t=\frac{60}{40}=\frac{3}{2}\;\mathrm{s}}\)

Położenie cząstek w chwili \(\displaystyle{t=\frac{3}{2}\;\mathrm{s}}\) wynosi:
\(\displaystyle{\vec{r}_A (t)=(-5+2\cdot\frac{3}{2})\,\hat{i}=-2\,\hat{i}\;\mathrm{km}}\)
\(\displaystyle{\vec{r}_B (t)=(-5+4\cdot\frac{3}{2})\,\hat{j}=1\,\hat{j}\;\mathrm{km}}\)

Informacja

Poniżej znajduje się prezentacja przemieszczeń cząstek w czasie od \(t=0\,\mathrm{s}\) do \(t=2\,\mathrm{s}\).

Możesz oglądać kolejne etapy ruchu cząstek, uruchamiając poszczególne etapy, za pomocą przycisków z numerami umieszczonych poniżej.

Odpowiedź

Wektor położenia cząstki \(A\) względem \(B\) wynosi \(\vec{r}_B-\vec{r}_A=\begin{bmatrix}(-5+2t)\hat{i}-(-5+4t)\hat{j} \end{bmatrix}\;\mathrm{km}\). Cząstki będą najbliżej siebie w chwili \(\displaystyle{t=\frac{3}{2}\,\mathrm{s}}\), a położenie ich w tej chwili opisywane jest wektorami: \(\vec{r}_A(t=1,5)=-2\,\hat{i}\;\mathrm{km}\) oraz \(\vec{r}_B(t=1,5)=1\,\hat{j}\;\mathrm{km}\).