Zadanie 2.2.2.1
Informacja
Możesz zobaczyć odpowiedź, klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- zależność położenia od czasu cząstki: \(x(t)=6\,t-\frac{1}{8}\,t^3 \mathrm{[m]}\).
Szukane:
- średnia szybkość cząstki w \(8\) pierwszych sekundach ruchu.
Odpowiedź
Średnia szybkość cząstki w pierwszych \(8\) sekundach ruchu wynosi \(\displaystyle{v_{śr}=6\,\mathrm{\frac{m}{s}}}\).
Polecenie
Poniżej przedstawiono dwie propozycje rozwiązania zadania. Wybierz drogę, która prowadzi do prawidłowego rozwiązania.
Należy policzyć położenie cząstki w pierwszej oraz ósmej sekundzie ruchu, a następnie skorzystać z definicji prędkości średniej.
Z równania opisującego ruch wynika, że cząstka może zmienić kierunek poruszania się na przeciwny, należy więc najpierw przeanalizować opisany ruch, a następnie obliczyć szybkość średnią uwzględniając zmiany kierunku ruchu.
Rozwiązanie
Do równania \(x(t)=6\,t-\frac{1}{8}\,t^3 \mathrm{[m]}\) można podstawić kolejne wartości czasu, aby otrzymać położenie cząstki, np.
\(x(1)=6\cdot\,1-\frac{1}{8}\cdot\,1^3 =6-\frac{1}{8}=5\frac{7}{8}\,\mathrm{m}\)
\(x(2)=11\,\mathrm{m}\)\(x(3)=14,625\,\mathrm{m}\)\(x(4)=16\,\mathrm{m}\)\(x(5)=14,375\,\mathrm{m}\)\(x(6)=9\,\mathrm{m}\)\(x(7)=-0,875\,\mathrm{m}\)\(x(8)=-16\,\mathrm{m}\)
Na podstawie wykonanych obliczeń można narysować wykres zależności drogi od czasu.
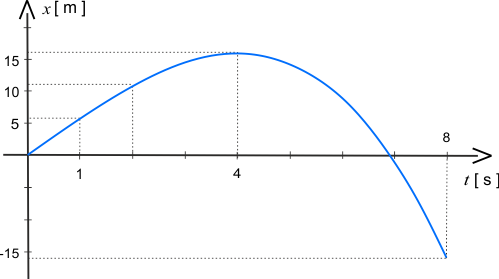
W czwartej sekundzie ruchu cząstka zmienia kierunek ruchu.
Polecenie
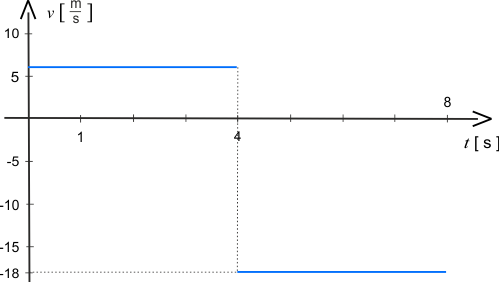
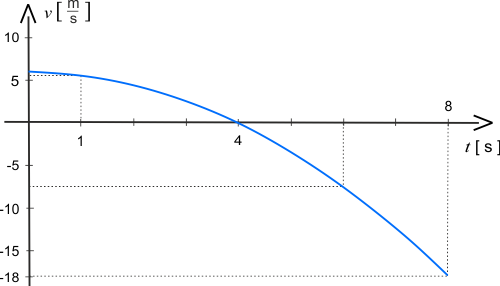
Poniżej przedstawione są dwa wykresy prędkości cząstki od czasu. Wybierz rysunek odpowiadający treści zadania.
gdzie:
\(\bigtriangleup x=x_{t2}-x_{t1}\) - położenie średnie,
\(\bigtriangleup t\) - przedział czasu.
Przykład:
Położenie cząstki opisane jest równaniem: \(x(t)=4\,t^2+2\,t\;\mathrm{[m]}\). Wyznacz wartość prędkości średniej pomiędzy \(2\) a \(4\) sekundą ruchu.
\(\displaystyle{v_{śr}=\frac{x(4)-x(2)}{4-2}}\)
\(\displaystyle{v_{śr}=\frac{4\cdot 4^2+2\cdot4-(4\cdot 2^2+2\cdot2)}{4-2}}=26\;\mathrm{\frac{m}{s}}\)
Rozwiązanie
Równanie opisujące szybkość poruszania się cząstki w zależności od czasu, można wyznaczyć z definicji szybkości chwilowej:
W czwartej sekundzie ruchu szybkość cząstki wynosi zero. W tym momencie cząstka wyhamowała i za chwilę rozpocznie ruch w przeciwną stronę.
Wartość szybkości średniej należy obliczyć osobno dla ruchów odbywających się w rożnych kierunkach.
Polecenie
Poniżej przedstawiono cztery wartości średnie szybkości cząstki. Wybierz jedną prawidłową wartość.
\[\displaystyle{v_{śr}=6\,\mathrm{\frac{m}{s}}}\]
\[\displaystyle{v_{śr}=3\,\mathrm{\frac{m}{s}}}\]
\[\displaystyle{v_{śr}=1,5\,\mathrm{\frac{m}{s}}}\]
\[\displaystyle{v_{śr}=-2,5\,\mathrm{\frac{m}{s}}}\]
Rozwiązanie
Analiza ruchu wykazała, że w \(4\) sekundzie zmianie ulega kierunek ruchu. Po tym czasie szybkości przyjmują wartości ujemne.
Szybkość średnią należy obliczyć osobno dla wartości dodatnich \(v_1\) i ujemnych \(v_2\).
Odpowiedź
Średnia szybkość cząstki w pierwszych \(8\) sekundach ruchu wynosi \(\displaystyle{v_{śr}=6\,\mathrm{\frac{m}{s}}}\).