Zadanie 2.3.1.6
Rzut poziomy i ukośny
Z wysokości \(10\,\mathrm{m}\) rzucono poziomo piłkę z prędkością \(\displaystyle{20\,\mathrm{\frac{m}{s}}}\). Wyznacz prędkość piłki po sprężystym odbiciu od poziomego podłoża oraz odległość między pierwszym a drugim miejscem uderzenia o nie. Przyspieszenie ziemskie wynosi \(\displaystyle{g=9,81\,\mathrm{\frac{m}{s^2}} }\).
Autor zadania: prof. inż. Jacek Własak
Wskazówka teoretyczna
Teoria - rzut poziomy
Współrzędne rzuconego poziomu ciała w pewnej chwili \(t\):
\( \eqalign{ x &= v_0 t \\ y &= h-\frac{1}{2} gt^2 } \)
Składowe wektora prędkości \(\vec{v}\) w pewnej chwili \(t\):
\( \eqalign{ v_x &= v_0 \\ v_y &= -gt } \)
Zasięg rzutu:
\(\displaystyle{OA=v_0\sqrt{\frac{2h}{g} } }\)
Czas trwania rzutu:
\(\displaystyle{t_{OA}=\sqrt{\frac{2h}{g}}}\)
Teoria - rzut ukośny
Rzut ukośny jest przykładem ruchu płaskiego. Jest to ruch o stałym przyspierzeniu \(\vec{g}\) i dowolnie skierowanej prędkości początkowej \(\vec{v}_0\).
Wartości składowe prędkości \(\vec{v}\) w dowolnej chwili \(t\):
Współrzędne ciała w dowolnej chwili \(t\):
Maksymalna wysokość rzutu:
Czas potrzebny na osiągniecie wysokości maksymalnej \(h\):
Zasięg rzutu:
Czas rzutu:
Wartości składowe prędkości \(\vec{v}\) w dowolnej chwili \(t\):
\(\eqalign{v_x &=v_0\cos \alpha \\ v_y &=v_0 \sin \alpha-gt}\)
Współrzędne ciała w dowolnej chwili \(t\):
\(\displaystyle{\eqalign{x &=v_0t\cos \alpha \\ y &=v_0t \sin \alpha- \frac{1}{2}gt^2}}\)
Maksymalna wysokość rzutu:
\(\displaystyle{h=\frac{v_0^2 \sin^2 \alpha}{2g}}\)
Czas potrzebny na osiągniecie wysokości maksymalnej \(h\):
\(\displaystyle{t=\frac{v_0 \sin \alpha}{g}}\)
Zasięg rzutu:
\(\displaystyle{0A=\frac{v_0^2 \sin 2\alpha}{g}}\)
Czas rzutu:
\(\displaystyle{t_{0A}=\frac{2v_0 \sin \alpha}{g}}\)
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- wysokość, z której rzucono piłkę \(h=10\,\mathrm{m}\),
- prędkość początkowa \(\displaystyle{v_0=20\,\mathrm{\frac{m}{s}}}\),
- przyspieszenie ziemskie \(\displaystyle{g=9,81\,\mathrm{\frac{m}{s^2}} }\).
Szukane:
- prędkość po sprężystym odbiciu od poziomego podłoża \(\vec{v}\),
- odległość między pierwszym a drugim miejscem uderzenia od podłoża \(\Delta x\).
Analiza sytuacji
Ciało oddziałuje z Ziemią grawitacyjnie. W pobliżu Ziemi siła grawitacyjna w dobrym przybliżeniu jest stała i wyrażamy ją wzorem \(\vec{F}=m\vec{g}\), nazywając natężenie pola natężenie pola grawitacyjnego Ziemi \(g\) przyspieszeniem ziemskim. W pobliżu Ziemi działa także siła oporu powietrza, ale ją pomijamy.
Sposób I - równania ruchu
Masa ciała jest stała, więc równanie ruchu uzyskujemy z drugiej zasady dynamiki w postaci:
\(\displaystyle{\vec{a}=\frac{\vec{F}}{m}}\)
Po wstawieniu siły \(\vec{F}=m\vec{g}\), otrzymujemy: \(\vec{a}=\vec{g}\). Jak widać ruch jest jednostajnie przyspieszony z przyspieszeniem \(\vec{g}\).
Rozwiązania równania ruchu, czyli równanie toru i równanie na prędkość, mają postać:
\(\displaystyle{\vec{r}=\vec{r}_0+\vec{v}_0t+\frac{1}{2}\vec{g}t^2}\)
\(\vec{v}=\vec{v}_0+\vec{g}t\)
gdzie \(\vec{r}_0\) i \(\vec{v}_0\) są odpowiednio położeniem i prędkością w chwili \(t=0\).
Ruchy, w których występuje niezerowa prędkość początkowa nazywamy rzutami, a w przypadku, gdy prędkość początkowa wynosi zero, mówimy o spadku swobodnym.
Początkowy ruch piłki jest rzutem poziomym, a po odbiciu od ziemi rzutem ukośnym.
Wybieramy kartezjański układ odniesienia o osi \(y\) skierowanej pionowo do góry i osi \(x\) skierowanej wzdłuż wektora prędkości początkowej, wtedy \(\vec{g}=(0,-g,0)\), \(\vec{v}=(v_0,0,0)\) i \(\vec{r_0}=(0,h,0)\). Równania toru dla ruchu poziomego w tym układzie współrzędnych mają postać:
- postać parametryczna \(x=v_0t\), \(\displaystyle{y=h-\frac{gt^2}{2} }\)
- postać jawna \(\displaystyle{y=h-\frac{gx^2}{2v_0^2} }\), \(z=0\) (tzn. ruch jest płaski).
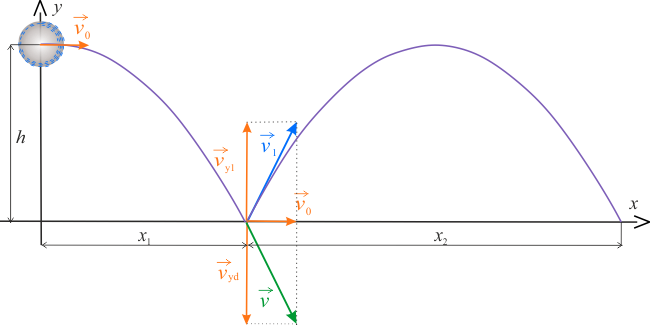
Czas \(t_1\) i miejsce \(x_1\) pierwszego odbicia znajdziemy podstawiając \(y=0\)
\(\displaystyle{0=h-\frac{gt_1^2}{2} }\)
\(\displaystyle{t_1=\sqrt{\frac{2h}{g}} }\)
\(\displaystyle{t_1=\sqrt{\frac{2\cdot 10}{9,81}}\approx1,43\,\mathrm{s} }\)
\(\displaystyle{x_1=v_0\sqrt{\frac{2h}{g}} }\)
\(\displaystyle{x_1=20\sqrt{\frac{2\cdot 10}{9,81}}\approx 28,57\,\mathrm{m} }\)
W zderzeniu sprężystym energia jest zachowana, stąd wartość prędkości nie zmieni się. Podczas odbicia składowa pozioma prędkości nie zmienia się, a pionowa mienia znak na przeciwny, stąd wynika, że kąt padania równa się kątowi odbicia. Składowe prędkości w punkcie zderzenia wynoszą:
\(\displaystyle{v_x=v_0=20\,\mathrm{\frac{m}{s}} }\)
\(\displaystyle{v_{yd}=-gt_1=-\sqrt{2gh}\approx -14\,\mathrm{\frac{m}{s}} }\)
Prędkość piłki po sprężystym odbiciu wynosi \(\displaystyle{\vec{v}=\left [20,14\right ]\,\mathrm{\frac{m}{s}} }\)
Równania toru rzutu ukośnego mają postać:
- postać parametryczna \(x=x_1+v_0t\), \(\displaystyle{y=v_{y1}t-\frac{gt^2}{2} }\)
- postać jawna \(\displaystyle{y=\frac{v_{y1}(x-x_1)}{v_0}-\frac{g(x-x_1)^2}{2v_0^2} }\), \(z=0\).
Miejsce drugiego upadku znajdujemy rozwiązując równanie kwadratowe dla \(y=0\)
\(\displaystyle{0=\frac{v_{y1}(x_2-x_1)}{2v_0}-\frac{g(x_2-x_1)^2}{2v_0^2} }\)
\[\displaystyle{0=2v_0v_{y1}(x_2-x_1)-g(x_2-x_1)^2 }\] \[2v_0v_{y1}=g(x_2-x_1)\] \[\displaystyle{\frac{2v_0v_{y1}}{g}=x_2-x_1}\] \[\displaystyle{x_2=x_1+v_0\frac{2}{g}gt_1 }\] \[\displaystyle{x_2=x_1+2v_0\sqrt{\frac{2h}{g}} }\]
\(x_2=x_1+2x_1=3x_1\)
Odległość między odbiciami wynosi \(\Delta x=x_2-x_1=2x_1\approx 57,14\,\mathrm{m} \)
Sposób II - zasada zachowania energii
Ponieważ siła \(mg\) jest zachowawcza, możemy korzystać z zasady zachowania energii mechanicznej.
W rozważanym ruchu zasadę zachowania energii przyjmuje postać:
\(\displaystyle{mgh+\frac{mv_0^2}{2}=\frac{m\left (v_{y1}^2+v_0^2\right )}{2} }\)
\(\displaystyle{mgh=\frac{mv_{y1}^2}{2} }\)
\(v_{y1}^2=2gh\)
\(v_{y1}^2=2gh\)
Prędkość po odbiciu wynosi
\(\vec{v}=(v_0,v_{y1})=\left (v_0,\sqrt{2gh}\right)\)
\(\displaystyle{\vec{v}=(20,14)\,\mathrm{\frac{m}{s}} }\)
Po odbiciu piłka wzniesie się na początkową wysokość, tam pionowa składowa prędkości zeruje się i piłka z poziomą prędkością \(v_0\) zacznie rzut poziomy taki sam, jak na początku.
Z równania na składową prędkości w ruchu do góry \(0=v_{y1}-gt_w\) wyliczamy czas wznoszenia \(t_w\):
\(\displaystyle{t_w=\sqrt{\frac{2h}{g}}=t_1 }\)
Zauważamy, że czas wznoszenia jest równy czasowi spadania, zatem czas lotu od pierwszego odbicia do drugiego wynosi \(2t_1\). W tym czasie, w poziomie, piłka przebędzie drogę:
\(x=v_02t_1\approx 57,14\,\mathrm{m}\)
Odpowiedź
Prędkość piłki po sprężystym odbiciu wynosi \(\displaystyle{\vec{v}=(20,14)\,\mathrm{\frac{m}{s}} }\). Odległość między odbiciami ma wartość \(\Delta x\approx 57,14\,\mathrm{m} \).