Zadanie 2.3.1.5
Wskazówka teoretyczna
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź. Na kolejnych zakładkach przedstawione są inne metody rozwiązania.
Dane i szukane
Dane:
- odległość pierwszej kartki od pistoletu \(x_1=20\ \mathrm{m}\),
- odległość drugiej kartki od pistoletu \(x_2=30\ \mathrm{m}\),
- różnica wysokości między pierwszym a drugim otworem po kuli \(\Delta y=0,05\ \mathrm{m}\),
- wartość przyspieszenia ziemskiego \(\displaystyle{10\,\mathrm{\frac{m}{s^2}}}\).
Szukane:
- prędkość początkowa kuli \(v_0\).
Analiza sytuacji
Pocisk będzie w trakcie lotu opadał pod wpływem sił grawitacji, czyli ruch będzie odbywał się do przodu i jednocześnie w dół. Jest to przykład ruchu poziomego. W rzucie poziomym ruch ciała można przedstawić jako złożenie ruchu jednostajnego z prędkością \(v_0\) w kierunku poziomym oraz ruchu jednostajnego przyspieszonego bez prędkości początkowej w kierunku pionowym (spadek swobodny).
W omawianym zadaniu najwygodniej jest obrać początek układu współrzędnych w miejscu początkowego ułożenia pocisku, czyli lufie pistoletu. Podejście takie eliminuje z rozważań wysokość ustawienia pistoletu w stosunku do podłoża. Uproszczenie takie można przyjąć jeśli nie interesuje nas zasięg ani czas trwania rzutu.
Na poniższym rysunku pokazano tor ruchu pocisku w opisanym układzie współrzędnych. Punktami \(A\) i \(B\) oznaczono miejsce przebicia kartek przez pocisk.
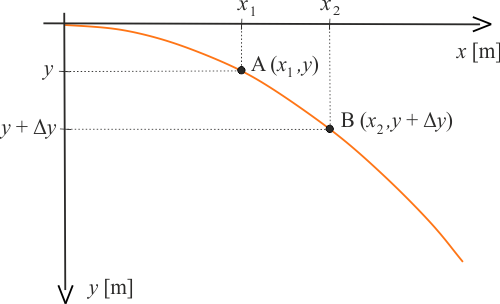
Początek toru pocisku umieszczono w początku układu współrzędnych, skąd narysowano łuk. Na trasie pocisku zaznaczone są dwie przegrody papierowe poprzez punkt \(A\) oraz punkt \(B\), oddalone od początku układu współrzędnych w odległościach odpowiednio \(x_1\) i \(x_2\). Zaznaczono także wysokość \(y\) oraz \(y+ \Delta y\) punktów przebicia obu kartek.
W treści zadania zostały podane informacje na temat położenia pocisku w dwóch chwilach czasu, dlatego też należy użyć równań opisujących położenie pocisku. Tak więc mamy dwa równania:
Z pierwszego równania łatwo jest wyznaczyć \(\displaystyle{t=\frac{x}{v_0}}\)
Następnie wyznaczone \(t\) podstawiane jest do drugiego równania:
Wyprowadzone równanie jest postaci \(y=ax^2\). Jest to parabola o \(\displaystyle{a=\frac{g}{2v_0^2}}\) mająca wierzchołek w początku układu współrzędnych.
Do takiej postaci równania można już podstawić współrzędne dwóch punktów \(A(x_1, y)\) oraz \(B(x_2, y+\Delta y)\).
\[\left\{\begin{matrix} y &=\frac{\Large{g}}{\Large{2v_0^2}}x_1^2 \\ y+\Delta y &= \frac{\Large{g}}{\Large{2v_0^2}}x_2^2 \end{matrix}\right.\]
Otrzymany układ równań można rozwiązać metodą podstawiania lub odejmując od drugiego równania pierwsze.
\[\left\{\begin{matrix} y &=\frac{\Large{g}}{\Large{2v_0^2}}x_1^2 \\ y+\Delta y &= \frac{\Large{g}}{\Large{2v_0^2}}x_2^2 \end{matrix}\right.\]
Odejmując od drugiego równania pierwsze otrzymujemy:
\(\displaystyle{y+\Delta y-y= \frac{g}{2v_0^2}x_2^2-\frac{g}{2v_0^2}x_1^2}\)
\(\displaystyle{\Delta y=\frac{g}{2v_0^2}(x_2^2-x_1^2)}\)
Otrzymane równanie obustronnie mnożymy przez czynnik \(\displaystyle{\frac{v_o^2}{\Delta y}}\)
\(\displaystyle{v_0^2 = \frac{g}{2\Delta y} (x_2^2-x_1^2)}\)
\(\displaystyle{v_0=\pm \sqrt{\frac{g}{2\Delta y}(x_2^2-x_1^2)}}\)
\[\left\{\begin{matrix} y &=\frac{\Large{g}}{\Large{2v_0^2}}x_1^2 \\ y+\Delta y &= \frac{\Large{g}}{\Large{2v_0^2}}x_2^2 \end{matrix}\right.\]
Do drugiego równania podstawiamy y wyznaczone w równaniu pierwszym.
\(\displaystyle{\frac{g}{2v_0^2}x_1^2+\Delta y = \frac{g}{2v_0^2}x_2^2}\)
Otrzymane równanie obustronnie mnożymy przez czynnik \(\displaystyle{\frac{v_o^2}{\Delta y}}\)
\(\displaystyle{\frac{g}{2\Delta y}x_1^2+v_0^2 = \frac{g}{2\Delta y}x_2^2}\)
\(\displaystyle{v_0^2 = \frac{g}{2\Delta y}x_2^2-\frac{g}{2\Delta y}x_1^2}\)
\(\displaystyle{v_0^2 = \frac{g}{2\Delta y} (x_2^2-x_1^2)}\)
\(\displaystyle{v_0=\pm \sqrt{\frac{g}{2\Delta y}(x_2^2-x_1^2)}}\)
Rozwiązanie
Wyprowadzenie jednostek:
Z treści zadania wiemy, że pocisk został wystrzelony w jedną stronę – na rysunku przyjęto kierunek „w prawo”, więc nie interesuje nas przypadek lotu w lewo (wartość ujemna prędkości).
Odpowiedź
Prędkość początkowa pocisku wynosi \(\displaystyle{v_0=223,6 \mathrm{\frac{m}{s}}}\).
Zadanie 2.3.1.5
Wskazówka teoretyczna
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- odległość pierwszej kartki od pistoletu \(x_1=20\ \mathrm{m}\),
- odległość drugiej kartki od pistoletu \(x_2=30\ \mathrm{m}\),
- różnica wysokości między pierwszym a drugim otworem po kuli \(\Delta h=h_1-h_2=0,05\ \mathrm{m}\),
- wartość przyspieszenia ziemskiego \(\displaystyle{10\,\mathrm{\frac{m}{s^2}}}\).
Szukane:
- prędkość początkowa kuli \(v_0\).
Analiza sytuacji
Pocisk będzie w trakcie lotu opadał pod wpływem sił grawitacji, czyli ruch będzie odbywał się do przodu i jednocześnie w dół. Jest to przykład ruchu poziomego. W rzucie poziomym ruch ciała można przedstawić jako złożenie ruchu jednostajnego z prędkością \(v_0\), w kierunku poziomym oraz ruchu jednostajnego przyspieszonego, bez prędkości początkowej w kierunku pionowym (spadek swobodny).
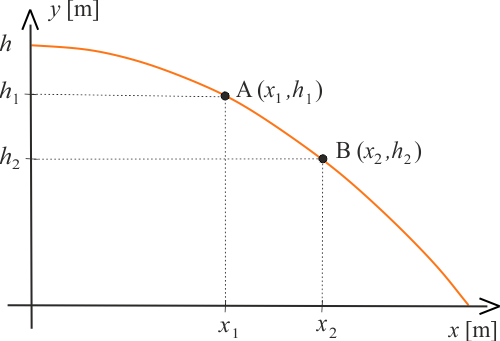
Początek toru pocisku umieszczono na pewnej wysokości w osi \(OY\), skąd narysowany jest łuk kończący się na osi \(OX\). Na trasie pocisku zaznaczono poprzez \(A\) i \(B\), punkty przebicia dwóch przegród papierowych.
Ruch wzdłuż osi \(OX\) można opisać ruch równaniem (droga w ruchu jednostajnym): \(x=v_0t\), stąd mamy:
Ruch wzdłuż osi \(OY\) można opisać ruch równaniem (odległość w ruchu jednostajnie przyspieszonym) \(\displaystyle{y=h-\frac{1}{2}gt^2}\), stąd mamy:
Obliczenia
\[\eqalign{\Delta h=& h-\frac{1}{2}gt_1^2-h+\frac{1}{2}gt_2^2 \\ \Delta h=& \frac{1}{2}g(t_2^2-t_1^2) \\ \Delta h=& \frac{1}{2}g(t_2-t_1)(t_2+t_1)\\ \Delta h=& \frac{1}{2}g\,\Delta t(t_2+t_1)\\ \Delta h=& \frac{1}{2}g\,\Delta t(t_2+t_1)}\]
Prędkość \(v_0\) jest wartością stałą, co oznacza, że \(\displaystyle{v_0=\frac{x_1}{t_1}=\frac{x_2}{t_2}}\) również \(\displaystyle{v_0=\frac{x_1+x_2}{t_1+t_2}}\) stąd mamy:
Podstawiając \(t_1+t_2\) do równania \(\displaystyle{\Delta t=\frac{2\Delta h}{g(t_2+t_1)}}\) mamy:\(\displaystyle{\Delta t=\frac{2\Delta hv_0}{g(x_1+x_2)}}\) stąd można wyznaczyć wielkość: \(\displaystyle{v_0=\frac{\Delta x}{\Delta t}}\),
\(\displaystyle{v_0=\frac{\Delta x}{\Delta t}=\frac{\Delta x\,g(x_1+x_2)}{2\Delta hv_0}}\) mnożąc stronami przez \(v_0\) mamy:\[\displaystyle{v_0^2=\frac{1}{2}\frac{\Delta x}{\Delta h}g(x_1+x_2)}\]
\(\displaystyle{v_0=\pm\sqrt{\frac{1}{2}\frac{(30-20)}{0,05}10\,(20+30)}=\pm223,61}\)
Wyprowadzenie jednostek:
Z treści zadania wiemy, że pocisk został wystrzelony w jedną stronę – na rysunku przyjęto kierunek „w prawo”, więc nie interesuje nas przypadek lotu w lewo (wartość ujemna prędkości).
Odpowiedź
Prędkość początkowa pocisku wynosi \(\displaystyle{v_0=223,6 \mathrm{\frac{m}{s}}}\).
Zadanie 2.3.1.5
Wskazówka teoretyczna
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- odległość pierwszej kartki od pistoletu \(x_1=20\ \mathrm{m}\),
- odległość drugiej kartki od pistoletu \(x_2=30\ \mathrm{m}\),
- różnica wysokości między pierwszym a drugim otworem po kuli \(\Delta h=0,05\ \mathrm{m}\),
- wartość przyspieszenia ziemskiego \(\displaystyle{10\,\mathrm{\frac{m}{s^2}}}\).
Szukane:
- prędkość początkowa kuli \(v_0\).
Analiza sytuacji
Pocisk będzie w trakcie lotu opadał pod wpływem sił grawitacji, czyli ruch będzie odbywał się do przodu i jednocześnie w dół. Jest to przykład ruchu poziomego. W rzucie poziomym ruch ciała można przedstawić jako złożenie ruchu jednostajnego z prędkością \(v_0\) w kierunku poziomym oraz ruchu jednostajnego przyspieszonego bez prędkości początkowej w kierunku pionowym (spadek swobodny).

Początek toru pocisku umieszczony został na pewnej wysokości w osi \(OY\), skąd narysowany jet łuk kończący się na osi \(OX\). Na trasie pocisku zaznaczono dwie przegrody papierowe poprzez punkt \(A\) oraz punkt \(B\), oddalone od początku układu współrzędnych w odległościach odpowiednio \(x_1\) i \(x_2\). Zaznaczono także wysokość \(h\) pomiędzy punktami przebicia obu kartek.
Z treści zadania wynika, że na podstawie dosyć dobrze opisanego toru pocisku, mamy określić jego prędkość początkową \(v_0\). Oba te elementy – tor oraz prędkość - łączą ze sobą równania ruchu. Musimy więc określić, jakiego typu ruchy wykonuje pocisk i podstawić wynikające z nich równania. Ruch odbywa się pod wpływem sił, dlatego zaczniemy od przyjrzenia się siłom działającym na pocisk:
- wystrzał z pistoletu powoduje przyłożenie do pocisku pewnej, nieznanej nam siły skierowanej poziomo. Siła ta nadaje mu prędkość początkową \(v_0\), ale znika po opuszczeniu przez pocisk lufy pistoletu,
- w trakcie lotu pocisku działa na niego siła grawitacji. Jej oddziaływanie powoduje opadanie pocisku, czyli pojawienie się prędkości skierowanej poziomo w dół. Zaraz po wystrzale ma ona wartość \(0\), ale nieustanny nacisk siły grawitacji cały powoduje jej przyrost,
- zgodnie z założeniami na pocisk nie działa siła oporu powietrza,
- podczas przechodzenia przez przegrody pocisk nie traci energii (zgodnie z założeniami), czyli żadna siła nie zmniejsza jego prędkości w tym momencie.
\[ \begin{matrix} \left\{\begin{matrix} x_1=v_0t_1 \\ h_1=\frac{gt_1^2}{2} \end{matrix}\right.& \mathrm{oraz} & \left\{\begin{matrix} x_2=v_0t_2 \\ h_2=\frac{gt_2^2}{2} \end{matrix}\right. \end{matrix} \]
Z powyższych wzorów znane są tylko wartości \(x_1\) oraz \(x_2\). Znacznie więcej jest wartości nieznanych: \(h_1, h_2, t_1, t_2\). Wprowadzone przez wzory nowe oznaczenia umieszczamy na rysunku. Dzięki wynikającej ze szkicu zależności \(h=h_2-h_1\) możemy pozbyć się nieznanych zmiennych \(h_1\) i \(h_2\) łącząc oba równania:
\[ h=\frac{gt_2^2}{2}-\frac{gt_1^2}{2}=\frac{g(t_2^2-t_1^2)}{2} \] Dzięki temu pozbywamy się dwóch nieznanych zmiennych \(h_1\) i \(h_2\).
Ostatecznie uzyskujemy następujący układ równań:
\[ \left\{\begin{matrix} \eqalign{ x_1 &= v_0t_1 \\ x_2 &= v_0t_2 \\ h&=\frac{g(t_2^2-t_1^2)}{2} } \end{matrix}\right. \]Uzyskany układ równań pozwala już na rozwiązanie zadania, gdyż przy trzech równaniach mamy w nim trzy niewiadome
Obliczenia
\[ \left\{\begin{matrix} \eqalign{ x_1 &= v_0t_1 \\ x_2 &= v_0t_2 \\ h&=\frac{g(t_2^2-t_1^2)}{2} } \end{matrix}\right. \]
Wykorzystując przekształcenia: \[ \eqalign{ x_1 &= v_0t_1 \Rightarrow t_1=\frac{x_1}{v_0} \\ x_2 &= v_0t_2 \Rightarrow t_2=\frac{x_2}{v_0} } \]
we wzorze na wysokość \(h\) obliczamy:
\[\displaystyle{h=\frac{g(t_2^2-t_1^2)}{2}}\]
\[ \eqalign{h &= \frac{g\left( \left (\frac{x_2}{v_0} \right )^2 - \left (\frac{x_1}{v_0} \right )^2\right )}{2} \\ h &= \frac{g\left ( \frac{x_2^2}{v_0^2} - \frac{x_1^2}{v_0^2} \right )}{2} \\ \frac{2h}{g} &= \frac{x_2^2}{v_0^2}-\frac{x_1^2}{v_0^2} \\ \frac{2h}{g} &= \frac{1}{v_0^2} \left (x_2^2-x_1^2 \right ) \\ v_0^2\frac{2h}{g} &= x_2^2-x_1^2 \\ v_0^2 &= \frac{g}{2h}\left (x_2^2-x_1^2 \right ) \\ v_0 &= \sqrt{\frac{g}{2h}\left (x_2^2-x_1^2 \right )} } \]
Po podstawieniu wartości liczbowych otrzymujemy:
\[\displaystyle{v_0=\sqrt{\frac{g}{2h}\left (x_2^2-x_1^2 \right )}\approx 223,6 \mathrm{\frac{m}{s}}}\]
\[\eqalign{ v_0=&\sqrt{\frac{10}{2\cdot0,05}\left (30^2-20^2 \right )\begin{bmatrix} \mathrm{\frac{\frac{\cancel{m}}{s^2}}{\cancel{m}} \left( m^2-m^2\right)}\end{bmatrix}}= \\& =\sqrt{100\cdot500\begin{bmatrix} \mathrm{\frac{1}{s^2}\cdot m^2} \end{bmatrix}}= \\& =\sqrt{50000\begin{bmatrix} \mathrm{\frac{m^2}{s^2}} \end{bmatrix}}\approx \\& \approx 223,6 \mathrm{\frac{m}{s}} }\]
Odpowiedź
Prędkość początkowa pocisku wynosi \(\displaystyle{v_0=223,6 \mathrm{\frac{m}{s}}}\)
