Analiza sytuacji

Szkicując zarys zadania musimy zastanowić się nad dwoma elementami: wyglądem zbocza oraz torem lotu pocisku. Na temat zbocza wiemy tylko tyle, że jest ono pochylone pod pewnym kątem do poziomu. Z braku innych danych możemy uznać, że jego profil jest linią prostą. Tor wystrzelonego pocisku ma kształt paraboli.

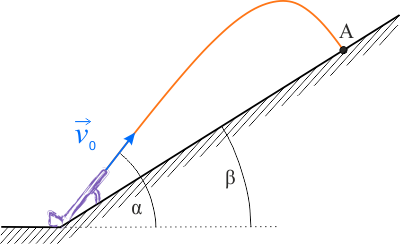
Kolejnym krokiem jest decyzja co do umieszczenia układu współrzędnych. Wybór ten ma wpływ na zapis równań matematycznych opisujących zachodzące w zadaniu zjawiska.
W naszym zadaniu ważne jest określenie miejsca, w którym powinien znaleźć się środek układu współrzędnych. Z treści zadania wiemy, że moździerz został ustawiony na początku zbocza. Oznacza to, że linia prosta obrazująca profil zbocza oraz parabola określająca tor lotu pocisku rozpoczynają się w tym samym punkcie. Punkt ten będzie idealnym miejscem do ustawienia układu współrzędnych.

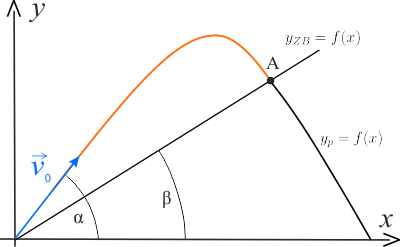
Zaznaczony na rysunku punkt \(A\) oznacza punkt uderzenia pocisku w zbocze. Znajduje się on na przecięciu paraboli obrazującej tor lotu pocisku oraz linii prostej obrazującej zbocze.

Rozwiązanie

Równanie prostej w postaci kierunkowej wygląda następująco:

gdzie współczynnik kierunkowy \(a=\operatorname{tg}{\beta}\) określa pochylenie prostej do poziomu, a wyraz wolny \(b\) określa przesunięcie linii w osi \(y\). Ponieważ linia oznaczająca tor lotu pocisku rozpoczyna się w punkcie \((0,0)\) układu współrzędnych, to \(b=0\). Ostatecznie funkcja opisująca profil zbocza wygląda następująco:


Tor ruchu w rzucie ukośnym jest określany przez dwa równania zależne od czasu: Pierwsze równanie przekształcamy tak, aby uzyskać wzór na \(t\), który następnie podstawiamy do drugiego równania  Jak?  \[\displaystyle{ x(t) = v_0\ t\,\cos\alpha \\ t = \frac{x}{v_0\, \cos\alpha} \\ y(t)= v_0\ t\,\sin\alpha - \frac{gt^2}{2} \\ y = \cancel{v_0}\ sin\alpha \frac{x}{\cancel{v_0}\,\cos\alpha} - \frac{g\left ( \frac{x}{v_0\,\cos\alpha} \right)^2}{2} = x\ \operatorname{tg}{\alpha} - \frac{g}{2} \frac{x^2}{v_0^2\ cos^2\alpha}} \]  Korzystając z równań na profil zbocza oraz tor lotu pocisku, można określić punkt uderzenia pocisku w zbocze \((x_A,y_A)\).
Punkt \(A\), oznaczający miejsce uderzenia pocisku w zbocze, jest wspólny dla obu funkcji, możemy więc zapisać powyższe równania konkretnie dla tego punktu: \[ \left\{\begin{matrix} \eqalign{ y_A^{ZB} &= x_A\ \operatorname{tg}{\beta} \\ y_A^P &= x_A\ \operatorname{tg}{\alpha} - \frac{g}{2} \frac{x_A^2}{v_0^2\,\cos^2\alpha} } \end{matrix}\right. \]
Podstawiając pierwsze równanie do drugiego, otrzymujemy po przekształceniach wzór na współrzędną \(x_A\) punktu uderzenia pocisku w zbocze:  Jak?  \[\eqalign{ x_A\ \operatorname{tg}{\beta} &=x_A\ \operatorname{tg}{\alpha}-\frac{g}{2}\frac{x_A^2}{v_0^2\,\cos^2\alpha}\\ \operatorname{tg}{\beta} &=\operatorname{tg}{\alpha}-\frac{g}{2}\frac{x_A}{v_0^2\,\cos^2\alpha}\\ \frac{g}{2}\frac{x_A}{v_0^2\,\cos^2\alpha} &=\operatorname{tg}{\alpha}-\operatorname{tg}{\beta}\\ g\ x_A &=2\ v_0^2\,\cos^2\alpha (\operatorname{tg}{\alpha}-\operatorname{tg}{\beta})\\x_A &=\frac{2\ v_0^2\,\cos^2\alpha (\operatorname{tg}{\alpha}-\operatorname{tg}{\beta})}{g}}\] 
\[ x_A = \frac{2}{g}\ v_0^2\,\cos^2\alpha (\operatorname{tg}{\alpha} - \operatorname{tg}{\beta)} \]
Otrzymany wzór podstawiamy do pierwszego równania, skąd do przekształceniach uzyskujemy wzór na współrzędną \(y_A\): \[ \eqalign{ y_A &= x_A\ \operatorname{tg}{\beta} = \\ &= \frac{2 v_0^2\,\cos^2\alpha \left ( \operatorname{tg}{\alpha} - \operatorname{tg}{\beta} \right ) }{g}\ \operatorname{tg}{\beta} } \]