Analiza sytuacji

Zacznijmy od określenia toru ruchu, na który podstawowy wpływ ma wektor prędkości spadającej paczki \(v\). Wektor ten zmienia się cały czas podczas opadania ładunku, przez co jest trudny do analizowania. Dlatego wspomnianą prędkość rozbijemy na dwie składowe skierowane wzdłuż osi układu współrzędnych \(v_x\) i \(v_y\). Ich zachowanie jest znacznie łatwiejsze do analizowania.

Ruch wzdłuż osi \(OX\) jest ruchem jednostajnym ze stałą prędkością:
\(v_x=v_0\)  oraz  \(x=v_0t\).

W kierunku osi \(OY\) występuje spadek swobodny z prędkością \(v_y=-gt\), a współrzędna położenia ciała na tej osi zależy od czasu w następujący sposób \(\displaystyle{y=h-\frac{1}{2}gt^2}\).

Prędkość pozioma pakunku \(v_x\) jest identyczna z prędkością lotu samolotu \(v_0\) przez cały czas spadania. Natomiast prędkość pionowa \(v_y\) pakunku ma w momencie wyrzucenia wartość \(0\), ale potem cały czas zwiększa się pod wpływem siły ciężkości. Opadający pakunek pod wpływem tych dwóch prędkości będzie się przemieszczał po torze o kształcie paraboli. Paczka nie spadnie w miejscu, w którym była wyrzucona. Miejsce upadku zostało zaznaczone punktem \(A\) (na rysunku poniżej), natomiast przez symbol \(d\) oznaczono odległość w poziomie między punktem wyrzucenia paczki a miejscem jej upadku.

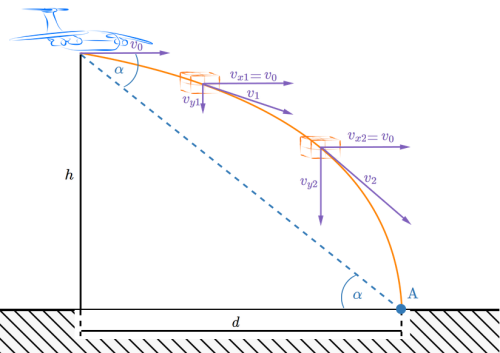
Rozwiązanie

Kąt \(\alpha\), szukany w zadaniu, można obliczyć korzystając z funkcji trygonometrycznej tangens. Aby jednak to zrobić, musimy wyliczyć wartość zmiennej \(d\).

Rzut poziomy traktować możemy jako złożenie spadku swobodnego z wysokości \(h\) oraz ruchu poziomego ze stałą prędkością \(v_0\). Zasięg \(d\) będzie równy:

gdzie \(t\) jest czasem ruchu, czyli czasem, który upłynął od upuszczenia ładunku do jego upadku na ziemię w punkcie \(A\). Czas ten można wyznaczyć na podstawie informacji, że w kierunku pionowym ruch ładunku jest spadkiem swobodnym z wysokości \(h\). Otrzymujemy:

Po przekształceniach mamy:
Obliczoną wartość podstawiamy do wzoru \(d=v_0t\) i otrzymujemy:
Mając obliczoną drogę \(d\) możemy określić kąt \(\alpha\):  Przekształcenia - etap 1  Podnosimy obie strony równania do drugiej potęgi w celu pozbycia się pierwiastka: \[ \eqalign{ (\operatorname{tg}{\alpha})^2 &= \frac{h^2}{v_0^2\frac{2h}{g}}= \\ &= h^\cancel{2}\frac{g}{2\cancel{h}v_0^2}= \\ &= \frac{hg}{2v_0^2} } \] 
 Przekształcenia - etap 2  Nakładamy na obie strony pierwiastek i mnożymy przez \(\sqrt{2}\): \[ \eqalign{ \operatorname{tg}{\alpha} &= \frac{\sqrt{hg}}{\sqrt{2}v_0}= \\ &= \frac{\sqrt{2}\sqrt{hg}}{2v_0}= \\ &= \frac{\sqrt{2hg}}{2v_0} } \] 
Po przekształceniach otrzymujemy: