Analiza sytuacji

Tor ruchu zbiornika można opisać następująco:

• zaraz po odłączeniu, zbiornik ma prędkość identyczną z prędkością rakiety, czyli \(v_1\),
• lecąc w górę zbiornik wytraca prędkość pod wpływem działania siły ciężkości, czyli porusza się ruchem jednostajnie opóźnionym – ruch ten znany jest jako rzut pionowy do góry z prędkością początkową \(v_1\),
• na wysokości \(h_2\) zbiornik kończy wznoszenie (prędkość wynosi \(0\)) i zaczyna swobodne opadanie,
• lecąc w dół, zbiornik cały czas przyspiesza pod wpływem działania siły ciężkości, czyli porusza się ruchem jednostajnie przyspieszonym – ruch ten znany jest jako spadek swobodny z wysokości \(h_2\),
• zbiornik uderza w ziemię z prędkością \(v_2\).

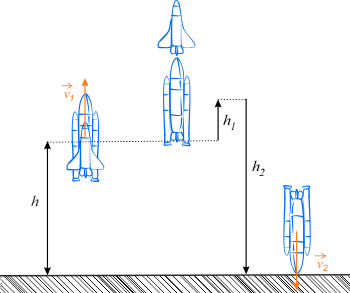
Tak opisany tor ruchu zbiornika przedstawiono na rysunku powyżej. Na podstawie podanej w treści informacji o pionowym wznoszeniu rakiety możemy przyjąć, że tor ruchu zbiornika (zarówno w górę jak i w dół) odbywa się po linii prostej. Dzięki temu nie musimy rozkładać prędkości zbiornika na składowe: poziomą i pionową.

Zadanie to można obliczyć na kilka sposobów. W rozwiązaniu podstawowym skorzystamy z prawa zachowania energii, a w komentarzu przedstawimy rozwiązanie alternatywne wykorzystujące właściwości ruchu jednostajnie zmiennego.

Rozwiazenie - metoda 1

Do obliczenia mamy dwie wartości: czas lotu zbiornika od momentu rozłączenia, do momentu upadku na ziemię \(t\) oraz prędkość, z jaką zbiornik uderzy w ziemię \(v_2\). Najlepiej będzie zacząć obliczenia od wyznaczenia prędkości \(v_2\).  Dlaczego?  Na tym etapie zadania trudno jest powiedzieć, którą niewiadomą należałoby obliczyć najpierw. W trakcie obliczeń okaże się, że aby obliczyć \(t\) konieczna będzie znajomość \(v_2\). 

Skorzystamy z prawa zachowania energii. Zgodnie z nim, w układzie izolowanym suma wszystkich rodzajów energii jest stała i zmieniać się może jedynie forma energii. Uogólniając to prawo do naszego zadania, można powiedzieć, że ruch ciała w polu grawitacyjnym w przypadku braku innych sił niż siła ciężkości, powoduje zmianę energii potencjalnej w kinetyczną i odwrotnie. Pole grawitacyjne jest polem sił zachowawczych i w przypadku braku innych sił zewnętrznych (np. sił oporu) w każdym punkcie pola energia jest stała (zachowana, jednakowa). Dla uproszczenia obliczeń przyjmiemy poziom gruntu jako poziom odniesienia we wzorach na energię potencjalną.

Aby wykorzystać prawo zachowania energii w zadaniu, musimy znaleźć punkty na torze ruchu zbiornika, których stan możemy dokładnie określić. W naszym przypadku znamy trzy takie punkty:

1. Punkt odłączenia od rakiety: zbiornik ma jakąś energię potencjalną \(E_p\) (znajduje się na pewnej wysokości nad ziemią \(h>0\) ) oraz kinetyczną \(E_k\) (porusza się z pewną prędkością \(v_1>0\) ),
2. Punkt zakończenia wznoszenia: zbiornik posiada energię potencjalną \(E_p\) oraz posiada energię kinetyczną równą zero \(E_k=0\) (\(v=0\), gdyż zakończył wznoszenie, a jeszcze nie zaczął opadać),
3. Punkt tuż przed zderzeniem z ziemią: zbiornik nie posiada energii potencjalnej \(E_p\) (gdyż znajduje się prawie na poziomie gruntu \(h\approx 0\)), lecz posiada energię kinetyczną \(E_k\) (spadając, rozpędził się do pewnej prędkości \(v_2>0\)).

Do utworzenia równania użyjemy punktów pierwszego i trzeciego. W punkcie pierwszym zbiornik ma energię całkowitą równą:
Natomiast w punkcie trzecim zbiornik ma energię całkowitą równą:

Korzystając z prawa zachowania energii, możemy zapisać:

Ponieważ znamy \(m\), \(g\), \(h\) i \(v_1\), to niewiadomą jest tylko \(v_2\). Po przekształceniach uzyskujemy wzór na obliczenie pierwszej niewiadomej.
 Przekształcenia  \[ \eqalign{ mgh+\frac{mv_1^2}{2} &= \frac{mv_2^2}{2} \\ 2mgh+mv_1^2 &= mv_2^2 \\ \cancel{m}(2gh+v_1^2) &= \cancel{m}v_2^2 \\ v_2 = \sqrt{2gh+v_1^2} } \] 

Do obliczenia pozostała nam już tylko jedna niewiadoma: czas lotu zbiornika od momentu rozłączenia do momentu upadku na ziemię \(t\).

Zgodnie z rysunkiem zbiornik porusza się kolejno dwoma ruchami: jednostajnie opóźnionym z prędkością początkową \(v_1\) i jednostajnie przyspieszonym z prędkością początkową \(0\). Całkowity czas opadania zbiornika na ziemię będzie, więc suma czasów obu tych ruchów \(t=t_w+t_{op}\), gdzie \(t_w\) to czas wznoszenia, a \(t_{op}\) to czas opadania.

Podstawiając do ogólnego wzoru na prędkość w ruchu jednostajnie opóźnionym \(v(t)=v_0-at\) symbole z zadania uzyskujemy:  Jak?  Zbiornik na końcu wznoszenia zatrzymuje się, więc prędkość końcowa wynosi \(v(t)=0\). Ponadto, prędkość początkowa \(v_0\) z wzoru ogólnego w zadaniu, oznaczona jest przez \(v_1\). 
Analogicznie, podstawiając do ogólnego wzoru na prędkość w ruchu jednostajnie przyspieszonym \(v(t)=v_0+at\), symbole z zadania uzyskujemy:  Jak?  Zbiornik w momencie zderzenia leci z prędkością końcową \(v(t)=v_2\). Ponadto prędkość początkowa \(v_0\) jest równa \(0\). 
Znając powyższe czasy, możemy określić sumaryczny czas lotu zbiornika:

Rozwiazenie - metoda 2

Zadanie można obliczyć także bez korzystania z prawa zachowania energii . Wystarczy znajomość właściwości ruchu jednostajnie zmiennego.

Pierwszy etap lotu zbiornika odbywa się na zasadach ruchu jednostajnie opóźnionego z prędkością początkową \(v_1\) i prędkością końcową \(0\). Podstawiając te dane do ogólnego wzoru na prędkość w ruchu jednostajnie opóźnionym \(v(t)=v_0-at\) i przekształcając go, otrzymujemy czas \(t_1\), po którym zakończy się wznoszenie zbiornika:

Korzystając z ogólnego wzoru na drogę w ruchu jednostajnie opóźnionym \(\displaystyle{s(t)=v_0t - \frac{at^2}{2} }\) i przekształcając go otrzymujemy drogę \(h_1\), którą przeleciał zbiornik w czasie wznoszenia:
Drugi etap lotu zbiornika odbywa się na zasadach ruchu jednostajnie przyspieszonego z prędkością początkową \(0\) i prędkością końcową \(v_2\). Korzystając z ogólnego wzoru na prędkość w ruchu jednostajnie przyspieszonym \(\displaystyle{s(t)=v_0t+\frac{at^2}{2}}\), możemy po przekształceniach otrzymać czas upadku zbiornika \(t_2\):

Wysokość \(h_2\), z której opada zbiornik zgodnie z rysunkiem powyżej określa zależność \(h_2 = h + h_1\). Podstawiając ją do poprzedniego wzoru otrzymujemy:
Całkowity czas opadania zbiornika \(t\) wynosi: Znając czas opadania zbiornika \(t_2\), można na podstawie ogólnego wzoru na prędkość w ruchu jednostajnie przyspieszonym określić prędkość \(v(t)=v_0+at\), w momencie uderzenia w ziemię: