Zadanie 2.4.1.1
  1. Ewa Frączek. Kurs obliczeniowy z fizyki.
  2. 2. Kinematyka
  3. 2.4. Ruch krzywoliniowy
  4. 2.4.1 Nauka
  5. Zadanie 2.4.1.1
DOI: 10.37190/OZE-FizykaCw1-r2

 Zadanie 2.4.1.1

Ruch po okręgu
Dwa owady chodzą po oponie rowerowej z tą samą prędkością liniową. Jeden z nich krąży po okręgu o promieniu \(r_1=0,5\,\mathrm{m}\), natomiast drugi zatacza okrąg o promieniu \(r_2=0,4\,\mathrm{m}\).
a) Oblicz stosunek prędkości kątowych tych owadów,
b) Tym razem jeden z owadów przyspieszył i po chwili poruszał się ze stałą prędkością. Okres przejścia mniejszego okręgu wynosi \(4\) minuty, a większego \(6\) minut. Ile wynosi stosunek prędkości liniowych oraz przyspieszeń dośrodkowych owadów?

 Wskazówka teoretyczna

 Teoria - ruch po okręgu
Przyspieszenie w ruchu po okręgu:

\(\vec{a}=\vec{a}_s+\vec{a}_d\)
\(a_s=\varepsilon R\)
\(\displaystyle{\varepsilon=\frac{\mathrm{d}\omega}{\mathrm{d}t}=\frac{\mathrm{d}^2\varphi}{\mathrm{d}t^2}}\)
\(\displaystyle{a_d=\omega ^2 R=\frac{v^2}{R}}\)
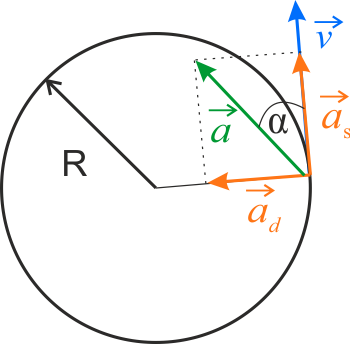
\(\displaystyle{\operatorname{tg}{\alpha}={\frac{a_d}{a_s}}}\)
\(\displaystyle{T=\frac{2\pi}{\omega}=\frac{1}{f}}\)
Wektory przyspieszenia

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
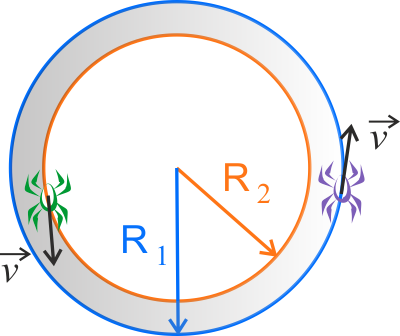
- promień większego okręgu \(R_1=0,5\,\mathrm{m}\),
- promień mniejszego okręgu \(R_2=0,4\,\mathrm{m}\),
Część b)
- okres owada pierwszego \(T_1=6\) minuty \(=360\,\mathrm{s}\),
- okres owada drugiego \(T_2=4\) minut \(=240\,\mathrm{s}\).

Szukane:
Część a)
- stosunek prędkości kątowych tych owadów: \(\displaystyle{\frac{\omega_1}{\omega_2}}\),
Część b)
- stosunek prędkości liniowych tych owadów: \(\displaystyle{\frac{v_1}{v_2}}\),
- stosunek przyspieszeń dośrodkowych owadów: \(\displaystyle{\frac{a_{d1}}{a_{d2}}}\).

Owady krążą po dwóch okręgach z tą samą prędkością liniową. Sytuację tę przedstawia poniższy rysunek.
Krążące owady

a) rozwiązanie

Prędkość kątową opisuje zależność: \(\displaystyle{\omega=\frac{v}{R}}\).
Dla owada pierwszego mamy: \(\displaystyle{\omega_1=\frac{v}{R_1}}\), natomiast dla drugiego: \(\displaystyle{\omega_2=\frac{v}{R_2}}\).
Stosunek prędkości kątowych tych owadów wynosi:

\(\displaystyle{\frac{\omega_1}{\omega_2}=\frac{v}{R_1}\frac{R_2}{v}=\frac{R_2}{R_1}=\frac{0,4}{0,5}=0,8}\)

b) rozwiązanie

Stosunek prędkości liniowych obu owadów wynosi:

\(\displaystyle{\frac{v_1}{v_2}=\frac{\omega_1R_1}{\omega_2R_2}=\frac{\frac{2\pi}{T_1}R_1}{\frac{2\pi}{T_2}R_2}=\frac{2\pi}{T_1}\cdot \frac{T_2}{2\pi}\cdot \frac{R_1}{R_2}}\)
\(\displaystyle{\frac{v_1}{v_2}=\frac{240}{360}\cdot \frac{0,5}{0,4}=\frac{5}{6}}\)

Stosunek przyspieszeń dośrodkowych owadów wynosi:
\(\displaystyle{\frac{a_{d1}}{a_{d2}}=\frac{\Large{\frac{v_1^2}{R_1}}}{\Large{\frac{v_2^2}{R_2}}}=\frac{R_2}{R_1}\cdot \left (\frac{v_1}{v_2}  \right )^2=\frac{4}{5}\cdot\left (\frac{5}{6}  \right )^2=\frac{5}{9}}\)

Odpowiedź

Stosunek prędkości kątowych tych owadów wynosi: \(\displaystyle{\frac{\omega_1}{\omega_2}=0,8}\).
Stosunek prędkości liniowych obu owadów wynosi: \(\displaystyle{\frac{v_1}{v_2}=\frac{5}{6}}\).
Stosunek przyspieszeń dośrodkowych owadów wynosi: \(\displaystyle{\frac{a_{d1}}{a_{d2}}=\frac{5}{9}}\).