Zadanie 2.4.1.5
  1. Kurs obliczeniowy z fizyki
  2. 2. Kinematyka
  3. 2.4. Ruch krzywoliniowy
  4. 2.4.1 Nauka
  5. Zadanie 2.4.1.5

 Zadanie 2.4.1.5

Analiza ruchu krzywoliniowego
Ruch cząsteczki opisuje wektor wodzący \(\displaystyle{\vec{r}=9\cos \left ( \frac{\pi }{3}t \right )\hat{i}+9\sin \left ( \frac{\pi }{3}t \right )\hat{j}}\,\mathrm{\left [m\right ]}\). Zbadaj ruch tej cząstki.

 Wskazówka teoretyczna

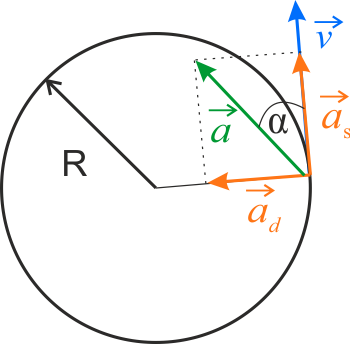
 Teoria - ruch po okręgu
Przyspieszenie w ruchu po okręgu:

\(\vec{a}=\vec{a}_s+\vec{a}_d\)
 
\(\displaystyle{\varepsilon=\frac{\mathrm{d}\omega}{\mathrm{d}t}=\frac{\mathrm{d}^2\varphi}{\mathrm{d}t^2}}\)
\(\displaystyle{a_s=\frac{\mathrm{d}v }{\mathrm{d} t}=\varepsilon R}\)
\(\displaystyle{a_d=\omega ^2 R=\frac{v^2}{R}}\)
\(\displaystyle{\operatorname{tg}{\alpha}={\frac{a_d}{a_s}}}\)
Ruch po okręgu

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- wektor wodzący cząstki \(\displaystyle{\vec{r}=9\cos \left ( \frac{\pi }{3}t \right )\hat{i}+9\sin \left ( \frac{\pi }{3}t \right )\hat{j}}\)

Szukane:
- parametry opisujące ruch cząstki: prędkość, przyspieszenia, tor ruchu, prędkość kątowa, okres.

Rozwiazanie

Najprościej jest wyznaczyć wektor prędkości punktu. Wektor wodzący wynosi:

\(\displaystyle{\vec{r}=9\cos \left ( \frac{\pi }{3}t \right )\hat{i}+9\sin \left ( \frac{\pi }{3}t \right )\hat{j}}\)

Wektor prędkości wyznaczamy następująco:
\(\displaystyle{\vec{v}=\frac{\mathrm{d}\vec{r} }{\mathrm{d} t}=-9\cdot \frac{\pi}{3}\sin\left ( \frac{\pi}{3}t \right )\hat{i}+9\cdot \frac{\pi}{3}\cos\left ( \frac{\pi}{3}t \right )\hat{j}}\)
\(\displaystyle{\vec{v}=-3\pi\sin\left ( \frac{\pi}{3}t \right )\hat{i}+3\pi\cos\left ( \frac{\pi}{3}t \right )\hat{j}}\)
 
\[\left (\sin(x)\right )' =\cos(x)\] \[\left (\cos(x) \right )' =-\sin(x) \] \[ \left (f\left (g(x)\right )\right )' =f'\left (g(x)\right )\cdot g'(x)\] 

Wartość prędkości wynosi:
\(\displaystyle{v=\sqrt{v_x^2+v_y^2}=\sqrt{\left (-9\cdot \frac{\pi}{3}\sin\left ( \frac{\pi}{3}t \right )\right )^2+\left (9\cdot \frac{\pi}{3}\cos\left ( \frac{\pi}{3}t  \right )  \right )^2}=3\pi}\,\mathrm{\frac{m}{s}}\)
 
\[\displaystyle{v=\sqrt{(-3\pi)^2 \sin^2 \left ( \frac{\pi}{3}t\right ) +(3\pi)^2 \cos^2 \left ( \frac{\pi}{3}t \right )}}\] \[\displaystyle{v=3\pi\sqrt{ \sin^2 \left (\frac{\pi}{3}t\right ) +\cos^2 \left (\frac{\pi}{3}t \right )}=3\pi\sqrt{1}=3\pi}\] 

Prędkość cząstki wynosi \(v=3\pi\,\mathrm{\frac{m}{s}}\). Jest to wartość stała. Kierunek prędkości wyznacza wektor jednostkowy:

\(\displaystyle{\vec{n_v}=-\sin\left ( \frac{\pi}{3}t \right )\hat{i}+\cos\left ( \frac{\pi}{3}t \right )\hat{j}}\)

Przyspieszenie punktu obliczamy z zależności:
\(\displaystyle{\vec{a}=\frac{\mathrm{d}\vec{v} }{\mathrm{d}t} =-3\pi\frac{\pi}{3}\cos\left ( \frac{\pi}{3}t \right )\hat{i}-3\pi\frac{\pi}{3}\sin\left ( \frac{\pi}{3}t \right )\hat{j}}\)
\(\displaystyle{\vec{a}=-\pi^2\cos\left ( \frac{\pi}{3}t \right )\hat{i}-\pi^2\sin\left ( \frac{\pi}{3}t \right )\hat{j}}\)
Wartość przyspieszenia wynosi:
\(\displaystyle{a=\sqrt{a_x^2+a_y^2}=\sqrt{\left (-\pi^2\cos\left ( \frac{\pi}{3}t \right )\right )^2+\left (-\pi^2 \sin\left ( \frac{\pi}{3}t \right ) \right )^2}=\pi^2}\,\mathrm{\frac{m}{s^2}}\)

Przyspieszenie oraz prędkości są stałe (nie zależą od czasu). Wektory prędkości oraz przyspieszenia zmieniają kierunek w czasie ruchu - w ich zapisie występuje zmienna \(t\). Cechy te wskazują na ruch po okręgu. W ruchu po okręgu składowa styczna przyspieszenia ma wartość zero, zaś składowa normalna \(a_d\) jest niezerowa:

\(\displaystyle{a_s=\frac{\mathrm{d} v}{\mathrm{d}t}=\frac{\mathrm{d} \,3\pi}{\mathrm{d}t}=0}\)  oraz  \(\displaystyle{a_d=\sqrt{a^2-a_s^2}=\sqrt{\pi^4-0}=\pi^2}\,\mathrm{\frac{m}{s^2}}\)

Przyspieszenie dośrodkowe można zapisać również następująco:
\(\displaystyle{a_d=\frac{v^2}{R}=\pi^2}\)
\(\displaystyle{R=\frac{v^2}{a_d}=\frac{9\pi^2}{\pi^2}=9\,\mathrm{m}}\)

Promień krzywizny toru ruchu określa zależność \(\displaystyle{R=\frac{v^2}{a_d}}\). Wartość promienia jest stała \(R=9\,\mathrm{m}\) oraz nie posiada składowej zetowej. Cechy te wskazują na ruch jednostajny po okręgu.

Prędkość kątową można wyznaczyć z zależności:
\(\displaystyle{\omega=\frac{v}{R}=\frac{3\pi}{9}=\frac{\pi}{3}\,\mathrm{\frac{rad}{s}}}\)

Okres w ruchu po okręgu obliczamy następująco:
\(\displaystyle{T=\frac{2\pi}{\omega}=\frac{2\pi}{\frac{\pi}{3}}=2\pi\frac{3}{\pi}=6\,\mathrm{s}}\)

Odpowiedź

Wektor prędkości wynosi: \(\displaystyle{\vec{v}=-3\pi\sin\left ( \frac{\pi}{3}t \right )\hat{i}+3\pi\cos\left ( \frac{\pi}{3}t \right )\hat{j}}\), zaś jej wartość wynosi: \(\displaystyle{v=3\pi\,\mathrm{\frac{m}{s}}}\).
Wektor przyspieszenia ma następującą postać: \(\displaystyle{\vec{a}=-\pi^2\cos\left ( \frac{\pi}{3}t \right )\hat{i}-\pi^2\sin\left ( \frac{\pi}{3}t \right )\hat{j}}\), zaś jego wartość wynosi: \(\displaystyle{a=\pi^2\,\mathrm{\frac{m}{s^2}}}\).
Cząstka krąży po okręgu o promieniu krzywizny \(R=9\,\mathrm{m}\), z prędkością kątową wynoszącą \(\displaystyle{\omega=\frac{\pi}{3}\,\mathrm{\frac{rad}{s}}}\) oraz okresem \(T=6\,\mathrm{s}\).