Zadanie 3.1.1.1
Wskazówka teoretyczna
W inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.
Zgodnie z I zasadą dynamiki, suma sił działających na układ musi wynosić zero.
II zasada dynamiki
Jeśli siły działające na ciało nie równoważą się, to ciało porusza się z przyspieszeniem wprost proporcjonalnym do siły wypadkowej, a odwrotnie proporcjonalnym do masy ciała. \[ \vec{a} = \frac{ \sum \vec{F}_{w} } {m} \left[ \frac{m}{s^2} = \frac{N}{kg} \right] \]
III zasada dynamiki
Jeśli ciało \(A\) działa na ciało \(B\) pewną siłą (siłą akcji), to ciało \(B\) działa na ciało \(A\) siłą (siłą reakcji) o takiej samej wartości i kierunku, lecz przeciwnym zwrocie. \[ \vec{F}_{AB} = -\vec{F}_{BA} \]
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- masa ciężarka \( m=0,5 \ \mathrm{kg} \),
- długość sznura \( l=3 \ \mathrm{m} \),
- ugięcie sznura \( h=0,15 \ \mathrm{m} \).
Szukane:
- siła naprężenia sznura \(F_N\).
Rozwiązanie - krok 1
Analizę sytuacji, przedstawionej w zadaniu, rozpoczynamy od wykonania rysunku.
Pomiędzy dwiema ścianami rysujemy sznurek. Z powodu wiszącego na nim obciążenia, sznur będzie naciągnięty w dół. Informacja o miejscu powieszenia ciężarka, w połowie długości sznura, jest bardzo istotna i znacznie ułatwia rozwiązanie zadania. Oznacza bowiem, że siły działające na obie połówki sznura będą symetryczne, a przez to łatwiejsze do obliczenia. Oczywiście, założenie o symetrii sił‚ działających na lewą i prawą stronę sznura jest prawdziwe tylko wtedy, gdy jest on zawieszony poziomo.
Jeśli sznurek wisiałby nie poziomo, ale pod kątem, to kąty pomiędzy jego lewą i prawą częścią a siłą ciężkości, działającą pionowo w dół, byłyby różne. A ponieważ siły naprężenia działają wzdłuż sznura, to one także znajdowałyby się w różnych położeniach względem siły ciężkości, czyli nie byłyby symetryczne.
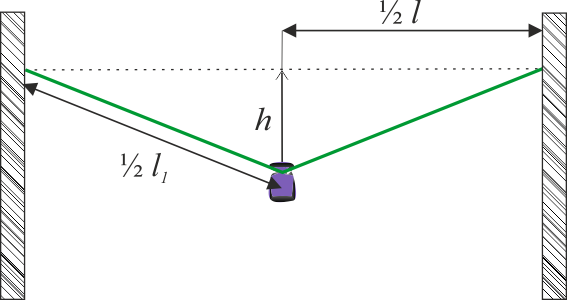
Wprowadzamy oznaczenia do rysunku. Zgodnie z danymi, odległość między dwoma ścianami wynosi \( l \). Skoro ciężarek zawieszony jest w połowie, to na rysunku wprowadzamy oznaczenia \(\displaystyle{ \frac{l}{2} }\). Zawieszenie ciężarka prowadzi do naciągnięcia sznura i powoduje obniżenie jego środka o wysokość \( h \). Skutkuje to pojawieniem się na rysunku nowej zmiennej oznaczonej jako \( \displaystyle{ \frac{l_1}{2}} \). Jest to długość połowy naciągniętego sznura.
Mając gotowy szkic obiektów możemy przystąpić do analizy układu. Na ciężarek działa siła ciężkości skierowana pionowo w dół i oznaczona jako \( mg \). Jej wartość jest równa masie ciężarka pomnożonej przez siłę przyciągania ziemskiego, a umocowana jest w punkcie zaczepienie ciężarka na sznurze.
Z treści zadania wiemy, że sznur jest nieważki. Oznacza to, że jego masa, a tym samym siły wprowadzane przez niego do układu, są tak niewielkie, iż można je pominąć bez szkody dla poprawności wyniku.
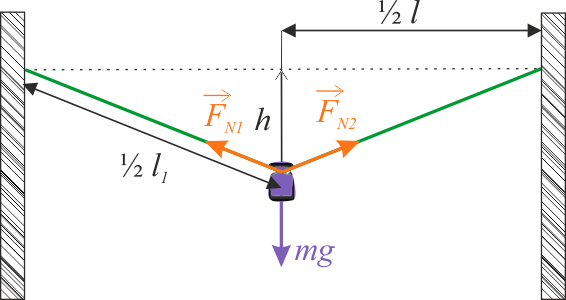
Po naciągnięciu sznura, pojawiają się w nim siły reakcji. Są one rozmieszczone wzdłuż osi sznura, na lewo i prawo od miejsca zawieszenia ciężarka. Oznaczamy je odpowiednio przez \( F_{N1} \) i \( F_{N2} \). Nie znamy ich wartości, a jedynie kierunki i zwroty. Ponadto, dzięki wspomnianemu wcześniej centralnemu zawieszeniu ciężarka, możemy powiedzieć, że są one symetryczne, czyli, co do wartości siły będą one sobie równe. \( \left | F_{N1} \right | = \left | F_{N2} \right | \).
Cały układ jest w stanie równowagi, więc zgodnie z I zasadą dynamiki, suma wektorowa sił działających na ciężarek musi być równa zeru, czyli \[ \sum {F} = 0 \].
Rozwiązanie - krok 2
Zgodnie z W inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym. , suma sił działających na układ musi wynosić zero. Graficzne przedstawienie tej zasady pokazane jest na rysunku poniżej. Złożenie wszystkich sił tworzy kontur zamknięty, czyli siły te wzajemnie się redukują.
W celu wykonania obliczeń należy rozłożyć siły działające w układzie na ich składowe leżące wzdłuż osi \(x\) i \(y\).
\[ \sum{F}=0 \Rightarrow \left\{\begin{matrix} \sum{F_X}=0 \\ \sum{F_Y}=0 \end{matrix}\right. \Rightarrow \left\{\begin{matrix} F_{N1x}-F_{N2x}=0 \\ F_{N1y}+F_{N2y}-mg=0 \end{matrix}\right. \]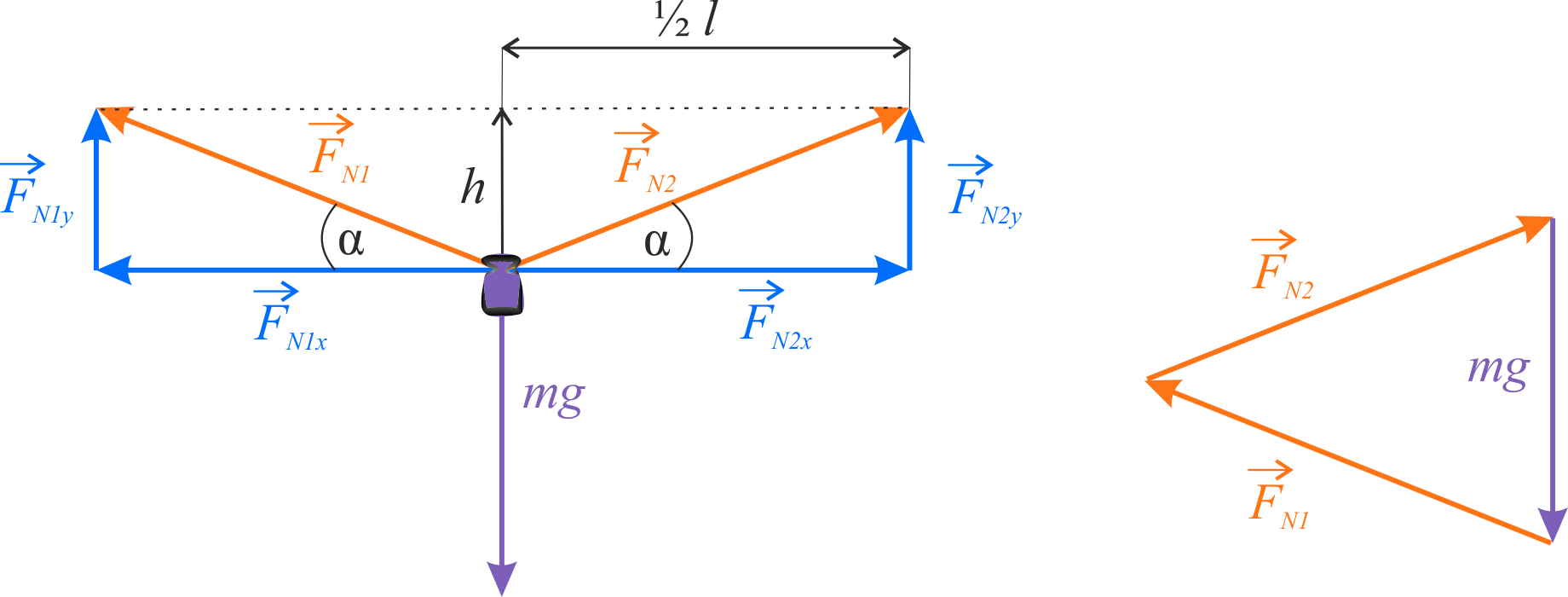
Równowaga sił wzdłuż osi \(x\) jest oczywista, gdyż w tym kierunku działają tylko składowe poziome sił naprężenia. Są one jednakowe ze względu na symetrię układu i w związku z tym wzajemnie się znoszą. Można więc pominąć je w obliczeniach. Natomiast wzdłuż osi \(y\) równowaga sił wymaga, aby siła ciężkości była równoważona przez dwie składowe pionowe sił naprężenia. Korzystając z wprowadzonego kąta \(\alpha \) (oznaczającego kąt pomiędzy naciągniętym sznurem a osią poziomą), przekształcamy siły składowe, działające wzdłuż osi \(y\) otrzymując: \[ F_{N1}\sin\alpha+F_{N2}\sin\alpha-mg=0 \]
Po Z powodu symetrii układu i równości, co do wartości sił \( F_{N1} \) i \( F_{N2} \), można powiedzieć, że składowe równoległe do osi \(y\) obu sił są identyczne: \[ F_{N1}\sin\alpha = F_{N2}\sin\alpha \] Dzięki temu można je zastąpić jedną niewiadomą \( F_N\sin\alpha \): \[ F_{N1}\sin\alpha + F_{N2}\sin\alpha = 2F_N\sin\alpha \] dostajemy: \[\eqalign{ 2F_N\sin\alpha-mg &= 0 \\ F_N &= \frac{mg}{2\sin\alpha} }\]
Sinus kąta \(\alpha \) obliczamy z trójkąta prostokątnego, zbudowanego przez wysokość ugięcia \(h\), połowę długości sznura przed ugięciem \( \displaystyle{\frac{l}{2}} \) oraz połowę długości sznura po ugięciu \(\displaystyle{\frac{l_1}{2}}\). Po Korzystając z wzoru na długość boku w trójkącie prostokątnym otrzymujemy: \[\eqalign{ h^2 + {\left( \frac{l}{2} \right) }^2 &= {\left( \frac{l_1}{2} \right) }^2 \\ \frac{l_1}{2} &= \sqrt {h^2 + {\left( \frac{l}{2} \right) }^2} }\] odcinka \(\displaystyle{ \frac{l_1}{2} }\) i podstawieniu wartości możemy zapisać: \[ \sin\alpha = \frac{h}{\frac{l_1}{2}} = \frac{h}{\sqrt {h^2 + {\left( \frac{l}{2} \right) }^2}} = \frac{0,15}{\sqrt {0,15^2 + {\left( \frac{3}{2} \right) }^2}} = 0,0995 \]
Mając obliczony kąt możemy wrócić do obliczania siły: \[ F_N=\frac{mg}{2\sin\alpha} =\frac{0,5\cdot 10}{2 \cdot 0,0995} \begin{bmatrix} \mathrm{kg \cdot \Large{\frac{m}{s^2}}} \end{bmatrix} =25,13\ \mathrm{N} \cong \mathbf {25\ \mathrm{N}} \]
Przybliżanie małych kątów
Dla małych kątów istnieje zależność mówiąca o tym, że miara kąta \(\alpha\) podana w radianach jest, co do wartości, zbieżna z wartościami sinusa i tangensa tego kąta, czyli: \[ \alpha \approx \sin\alpha \approx \tan\alpha \] Zależność ta jest prawdziwa tylko wtedy, kiedy wartość kąta jest podana w mierze łukowej (czyli w radianach). Wartość kąta w mierze łukowej określa się przez stosunek długości odcinka łuku \( l \) zakreślonego przez ten kąt do promienia tegoż łuku \( r \): \[ \alpha = \frac {l}{r} \] Dokładność tego przybliżenia jest różna dla różnych funkcji. Tabela poniżej przedstawia dokładność przybliżenia dla poszczególnych kątów.
| Funkcja tangens | Kąt \(\alpha\) | Funkcja sinus | |||
| błędy przybliżenia | \(\operatorname{tg}{(\alpha)}\) | \(\alpha [^{\circ}]\) | \(\alpha \mathrm{[rad]}\) | \(\sin(\alpha)\) | błędy przybliżenia |
| 0,00 % | 0,000000 | 0 | 0,000000 | 0,000000 | 0,00 % |
| 0,01 % | 0,017455 | 1 | 0,017453 | 0,017452 | 0,01 % |
| 0,04 % | 0,034921 | 2 | 0,034907 | 0,034899 | 0,02 % |
| 0,09 % | 0,052408 | 3 | 0,052360 | 0,052336 | 0,05 % |
| 0,16 % | 0,069927 | 4 | 0,069813 | 0,069756 | 0,08 % |
| 0,25 % | 0,087489 | 5 | 0,087266 | 0,087156 | 0,13 % |
| 0,37 % | 0,105104 | 6 | 0,104720 | 0,104528 | 0,18 % |
| 0,50 % | 0,122785 | 7 | 0,122173 | 0,121869 | 0,25 % |
| 0,65 % | 0,140541 | 8 | 0,139626 | 0,139173 | 0,33 % |
| 0,82 % | 0,158384 | 9 | 0,157080 | 0,156434 | 0,41 % |
| 1,02 % | 0,176327 | 10 | 0,174533 | 0,173648 | 0,51 % |
| 1,23 % | 0,194380 | 11 | 0,191986 | 0,190809 | 0,62 % |
| 1,47 % | 0,212557 | 12 | 0,209440 | 0,207912 | 0,73% |
| 1,72 % | 0,230868 | 13 | 0,226893 | 0,224951 | 0,86 % |
| 2,00 % | 0,249328 | 14 | 0,244346 | 0,241922 | 1,00 % |
Odpowiedź
Na każdą połowę sznura działa siła naprężenia o wartości \( 25 \ \mathrm{N} \).