Analiza sytuacji

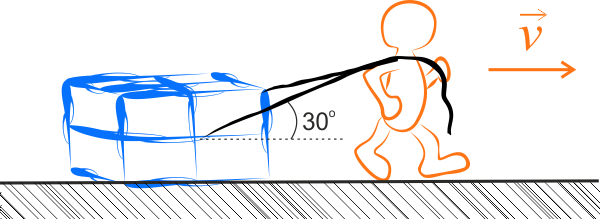
Na poruszającą się skrzynię, działają cztery siły, w wyniku których przesuwa się ona ze stałą prędkością po podłodze. Dwie z nich działają prostopadle do podłogi. Są to: siła ciężkości \(P\) oraz siła reakcji podłogi \(R\). Interesująca nas siła nacisku skrzyni na podłogę \(N\), zgodnie z III zasadą dynamiki, równa jest, co do wartości, sile \(R\) i jest przeciwlegle do niej skierowana.

Człowiek ciągnie za linę z siłą \(F\) równą sile naciągu liny \(F_N\), która to siła bezpośrednio działa na skrzynię. W kierunku przeciwnym do ruchu skrzyni działa siła tarcia kinetycznego \(T\). W wyniku działania tych sił, skrzynia przesuwana jest ze stałą prędkością po podłodze. Z I zasady dynamiki Newtona wynika, że suma wektorowa tych sił musi być równa \(0\).

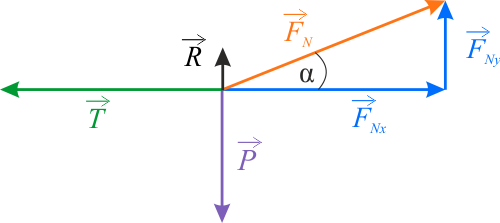
Diagram sił, działających na skrzynię, przedstawiono na rysunku powyżej. Na diagramie siły są reprezentowane przez ich wartości bezwzględne. Na diagramie siła naprężenia sznura została zastąpiona swoimi składowymi w kierunkach \(x\) i \(y\). Na diagramie nie ma, interesującej nas, siły nacisku skrzyni na podłogę \(N\).  Dlaczego?  Oddziaływanie grawitacyjne Ziemi powoduje, że na skrzynię działa siła ciężkości zależna od jej masy i skierowana pionowo w dół \(P=Mg\). Przyłożona do liny siła ciągnąca skrzynię, działa pod kątem \(30^{\circ}\) w górę, więc część tej siły próbuje unieść skrzynię. Jest ona zbyt mała żeby ją podnieść, jednak powoduje zmniejszenie nacisku na podłoże. Zgodnie z tym, siłę nacisku skrzyni na podłoże można określić wzorem: \[N=P-F_{Ny}\] 

Z pierwszej zasady dynamiki Newtona wynika, że suma wektorowa sił musi być równa zero, więc równanie wektorowe, wiążące wszystkie siły, ma postać:
\[ \vec{R}+\vec{P}+\vec{T}+\vec{F}_N=0 \]
Równanie to można zastąpić równoważnym układem dwu równań skalarnych. W tym celu rozłóżmy powyższe wektory w kartezjańskim układzie współrzędnych, którego oś \(OX\) jest skierowana równolegle do podłogi, a oś \(OY\) jest do niej prostopadła. W tak wybranym układzie współrzędnych warunek równowagi siły, działających na skrzynię, można zapisać jako:
\[ \eqalign{ \sum F_x &= F_{Nx} - T = 0 \\ \sum F_y &= F_{Ny} + R - P = 0 } \]
Rozpisując siłę tarcia oraz składowe siły naprężenia liny uzyskujemy:
\[\eqalign{ T &= \mu N \\ F_{Nx} &= F_N \cos \alpha \\ F_{Ny} &= F_N \sin \alpha } \]
Przyjmując, że zgodnie z III zasadą dynamiki, siła reakcji podłoża jest równa (co do wartości) sile nacisku skrzyni na podłoże, otrzymujemy zależność \(R=N\). Ponadto korzystając z faktu, że siła z jaką człowiek ciągnie linę, jest równa (co do wartości) sile naprężenia liny \(F=F_N\) otrzymujemy układ dwóch równań:
\[ \eqalign{ \sum F_x &= F \cos \alpha - \mu N = 0 \\ \sum F_y &= F \sin \alpha - Mg +N = 0 } \]

Rozwiązanie

\[ \eqalign{ \sum F_x &= F \cos \alpha - \mu N = 0 \\ \sum F_y &= F \sin \alpha - Mg + N= 0 } \]

W równaniach tych niewiadomymi są: siła z jaką człowiek ciągnie linę \(F\) oraz siła nacisku \(N\).

Po odpowiednich  przekształceniach  Przekształcamy drugie równanie, tak aby uzyskać wzór na siłę nacisku \(N\): \[ \eqalign{ F\sin \alpha + N - Mg &= 0 \\ N &= Mg - F\sin\alpha } \] Podstawiając go do pierwszego równania uzyskujemy: \[ \eqalign{ F\cos \alpha- \mu N &= 0 \\ F\cos\alpha - \mu (Mg- F\sin \alpha) &= 0 \\ F\cos\alpha-\mu Mg+\mu F\sin \alpha &= 0 \\ F(\cos\alpha+\mu \sin \alpha) &=\mu Mg \\ F &= \frac{\mu Mg}{\cos \alpha + \mu \sin \alpha} } \]  otrzymujemy wzór na siłę, z którą człowiek ciągnie linę:
\[ F = \frac{\mu Mg}{\cos \alpha + \mu \sin \alpha} \]
Podstawiając do niego dane, możemy wyliczyć wartość szukanej siły:
\[\displaystyle{F= \frac{0,3 \cdot 100 \cdot 10}{\frac{\sqrt{3}}{2} + 0,3 \cdot \frac{1}{2}} =  \frac{300}{\frac{0,3 + \sqrt{3}}{2}}\approx 295 \,\mathrm{N} } \]

Mając obliczoną siłę, z jaką człowiek ciągnie skrzynię, możemy powrócić do drugiego równania:
\[\displaystyle{N=Mg - F \sin \alpha =100 \cdot 10 - 295 \cdot \frac{1}{2}=852,5\, \mathrm{N} } \]
 Komentarz  Nie jest ważne, z jaką prędkością człowiek ciągnie skrzynię – siła jest taka sama. Człowiek ciągnąc skrzynię musi jednak uważać, aby ani na chwilę nie zatrzymać się, gdyż wtedy, aby znów nadać skrzyni prędkość, musi działać z większą siłą ze względu na to, że współczynnik tarcia statycznego pomiędzy skrzynią a podłogą jest większy niż współczynnik tarcia kinetycznego.