Zadanie 3.1.1.3
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.1. Zastosowanie I zasady Newtona
  4. 3.1.1 Nauka
  5. Zadanie 3.1.1.3

 Zadanie 3.1.1.3

Równowaga trzech sił
Trzech zawodników bawi się w przeciąganie liny. Liny są połączone w ten sposób, że jeden koniec każdej z nich jest związany we wspólnym węźle z pozostałymi. Zawodnicy: Wektorysław i Dynaminka ciągną swoje końce lin z siłami o wartościach odpowiednio \(400 \,\mathrm{N}\) i \(300\,\mathrm{N}\). Wiedząc, że węzeł łączący sznury nie porusza się, oraz że kąt między linami ciągniętymi przez Wektorysława i Dynaminkę wynosi \(120^{\circ}\) znajdź kierunek liny ciągniętej przez Fizaliusza oraz wartość siły, z jaką on ją ciągnie.

 Wskazówka teoretyczna

 Zasady dynamiki Newtona
I zasada dynamiki

W inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.
Zgodnie z  I zasadą dynamiki, suma sił działających na układ musi wynosić zero.

II zasada dynamiki

Jeśli siły działające na ciało nie równoważą się, to ciało porusza się z przyspieszeniem wprost proporcjonalnym do siły wypadkowej, a odwrotnie proporcjonalnym do masy ciała. \[ \vec{a} = \frac{ \sum \vec{F}_{w} } {m} \left[ \frac{m}{s^2} = \frac{N}{kg} \right] \]
III zasada dynamiki

Jeśli ciało \(A\) działa na ciało \(B\) pewną siłą (siłą akcji), to ciało \(B\) działa na ciało \(A\) siłą (siłą reakcji) o takiej samej wartości i kierunku, lecz przeciwnym zwrocie. \[ \vec{F}_{AB} = -\vec{F}_{BA} \]
Rysunek 1

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- siła, z jaką Wektorysław ciągnie linę \(F_A = 400 \ \mathrm{N}\),
- siła, z jaką Dynaminka ciągnie linę \(F_B = 300 \ \mathrm{N}\),
- kąt pomiędzy linami Wektorysława i Dynaminki \(\alpha = 120^{\circ} \).

Szukane:
- siła, z jaką Fizaliusz ciągnie linę \(F_C\),
- kąt pomiędzy linami Wektorysława i Fizaliusza \(\beta\).

Analiza sytuacji - rysunek

Zapisanie układu równań, dla warunków zadania, będzie prostsze, jeśli rozrysujemy siły działające na linę.

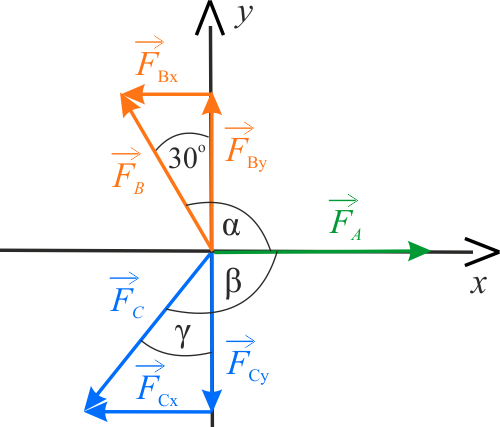
Rozkład sił

Na rysunku, układ współrzędnych został tak dobrany, aby jedna z sił działała wzdłuż osi \(OX\). Zabieg ten uprości układ równań, opisujących siły. Na rysunku został zaznaczony dodatkowy kąt \(\gamma\). Został on dodany, dla ułatwienia zapisu składowych siły \(\vec{F_C}\). Kąt ten można łatwo powiązać z katem \(\beta\) za pomocą wzoru \( \beta = \gamma + 90^{\circ}\).
Z rysunku można jeszcze odczytać, że:
\(\displaystyle{\sin 30^{\circ}=\frac{F_{Bx}}{F_B}}\)  oraz  \(\displaystyle{\cos 30^{\circ}=\frac{F_{By}}{F_B}}\)
\(\displaystyle{\sin \gamma=\frac{F_{Cx}}{F_C}}\)  oraz  \(\displaystyle{\cos \gamma=\frac{F_{Cy}}{F_C}}\)

Na podstawie informacji zawartych w zadaniu, można określić przybliżony kierunek i wartość siły przyłożonej do liny ciągniętej przez Fizaliusza. Skoro węzeł łączący wszystkie trzy liny nie porusza się, to układ musi być w równowadze, czyli siły narysowane na diagramie powinny tworzyć trójkąt.

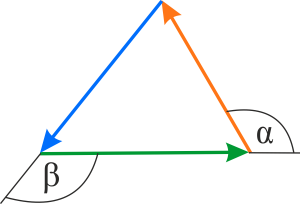
Rysunek 2

Analiza sytuacji

Zawarty, w I zasadzie dynamiki Newtona, warunek równowagi dla układu, zapiszemy w postaci wektorowej: \[ \vec{F_A} + \vec{F_B} + \vec{F_C} = 0 \] Po rozłożeniu sił na składowe równoległe do osi układu współrzędnych, możemy zapisać układ równań w postaci skalarnej: \[ \eqalign{ \sum F_x &= F_A- F_{Bx}-F_{Cx}= 0 \\ \sum F_y &= F_{By}-F_{Cy}= 0 } \]
\[\left\{\begin{matrix}F_A-F_B\sin 30^{\circ}-F_C\sin\gamma &=0\\F_B\cos 30^{\circ}-F_C\cos \gamma &=0\end{matrix}\right.\]

Obliczenia

\[\left\{\begin{matrix}F_A-F_B\sin 30^{\circ}-F_C\sin\gamma &=0\\F_B\cos 30^{\circ}-F_C\cos \gamma &=0\end{matrix}\right.\]
Przekształcając drugie równanie z podanego układu równań, otrzymujemy:
\[ F_C = \frac{F_B \cos 30^{\circ}}{\cos \gamma} \]
Podstawiając otrzymaną zależność do pierwszego równania i przekształcając, uzyskujemy:
\[ F_A - F_B \sin 30^{\circ} - \frac{F_B \cos 30^{\circ}}{\cos \gamma} \cdot \sin \gamma = 0 \\ F_A - F_B \sin 30^{\circ} = F_B \cos 30^{\circ} \cdot \frac{\sin \gamma}{\cos \gamma} \\ \operatorname{tg}{\gamma} = \frac{F_A - F_B \sin 30^{\circ}}{F_B \cos 30^{\circ}} \]
Wzór ten po podstawieniu danych pozwala obliczyć wartość kąta \(\gamma\):
\[\displaystyle{\operatorname{tg}{\gamma}=\frac{400-300 \cdot 0,5}{300 \cdot \frac{\sqrt{3}}{2}}=0,96225 }\]
Wartość kąta wynosi \(\gamma=44^{\circ}\)
Ostatecznie szukaną wartość kąta \(\beta\):
\[ \beta = \gamma +90^{\circ} = 44^{\circ} + 90^{\circ} = 134^{\circ} \]
Znając kąt \(\gamma\), można powrócić do wzoru na wartość siły \(F_C\) wyprowadzonego z układu równań:
\[ \displaystyle{ F_C = \frac{F_B \cos 30^{\circ}}{\cos 44} = \frac{300 \cdot \frac{\sqrt{3}}{2}}{0,71934} \approx 361 \mathrm{N} } \]

Odpowiedź

Kąt między liną Wektorysława a Fizaliusza wynosi \(134^{\circ}\), zaś siła, z jaką ciągnie line Fizaliusz, ma wartość \(F_C=361 \mathrm{N}\).

Informacja

Poniżej przedstawiona jest animacja, obrazująca zależności geometryczne pomiędzy wektorami siły. Pod animacja znajdują się granatowe, okrągłe przyciski z cyframi. Klikając w odpowiedni numer możesz oglądnąć kolejne etapy analizy geometrycznej.