Zadanie 3.1.1.4

Ruch po równi pochyłej

Skrzynia o masie

$50\,\mathrm{kg}$ porusza się ze stałą prędkością w górę rampy, będącej równią pochyłą, nachyloną pod kątem

$30^{\circ}$ do poziomu. Współczynnik tarcia między skrzynią a powierzchnią rampy wynosi

$0,2$ . Oblicz wartość poziomo skierowanej siły, z jaką należy działać na skrzynię wzdłuż jej toru ruchu, aby skrzynia poruszała się ze stałą prędkością

$\displaystyle{0,36\ \mathrm{\frac{km}{h}} }$ ?

Wskazówka teoretyczna

Zasady dynamiki Newtona

I zasada dynamiki

W inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.
Zgodnie z I zasadą dynamiki, suma sił działających na układ musi wynosić zero.

II zasada dynamiki

Jeśli siły działające na ciało nie równoważą się, to ciało porusza się z przyspieszeniem wprost proporcjonalnym do siły wypadkowej, a odwrotnie proporcjonalnym do masy ciała.

$\vec{a} = \frac{ \sum \vec{F}_{w} } {m} \left[ \frac{m}{s^2} = \frac{N}{kg} \right]$
III zasada dynamiki

Jeśli ciało

$A$ działa na ciało

$B$ pewną siłą (siłą akcji), to ciało

$B$ działa na ciało

$A$ siłą (siłą reakcji) o takiej samej wartości i kierunku, lecz przeciwnym zwrocie.

$\vec{F}_{AB} = -\vec{F}_{BA}$

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa skrzyni $m = 50\ \mathrm{kg}$ ,
- kąt nachylenia rampy $\alpha = 30^{\circ}$ ,
- współczynnik tarcia kinetycznego $\mu = 0,2$ ,
- prędkość skrzyni $\displaystyle{v = 0,36\ \mathrm{\frac{km}{h}}=0,1\,\mathrm{\frac{m}{s}}}$ .

Szukane:
- siła pchająca skrzynię $F$ .

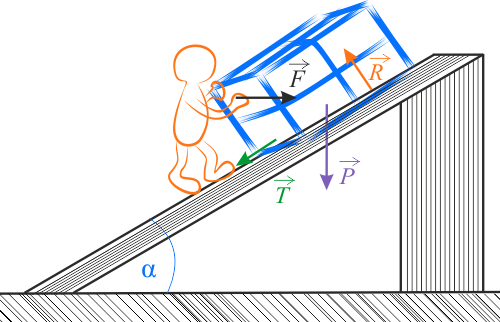
Analiza sytuacji

Na skrzynię, pchaną do góry po rampie, działają następujące siły:

siła ciężkości $\vec{P}$ , skierowana pionowo w dół i o wartości $mg$ ,
siła reakcji $\vec{R}$ , skierowana do góry, w kierunku prostopadłym do rampy,
siła wynikająca z tarcia kinetycznego $\vec{T}$ , działająca wzdłuż rampy w kierunku przeciwnym do wektora prędkości,
siła pchająca $\vec{F}$ , skierowana poziomo, równolegle do podłoża (nie rampy!).

Poniżej znajduje się rysunek z siłami działającymi na skrzynię. Układ współrzędnych został obrócony w celu uproszczeniu równań.

W zadaniach tego typu, dla ułatwienia obliczeń, najczęściej siły rozdziela się na dwie grupy: działające wzdłuż osi

$OX$ oraz wzdłuż osi

$OY$ . Gdyby układ współrzędnych był ustawiony standardowo (oś

$x$ poziomo, oś

$y$ pionowo), to z diagramu widać, że siły

$\vec{R}$ i

$\vec{T}$ należy rozbić na składowe.

$\eqalign{ T_x &= T \cos\alpha \\ T_y &= T \sin\alpha \\ R_x &= R \sin\alpha \\ R_y &= R \cos\alpha }$ Oznacza to, że nieznane siły

$T_x$ ,

$T_y$ ,

$R_x$ i

$R_y$ pojawią się w obu wzorach: na sumę sił w osi

$OX$ oraz sumę sił w osi

$OY$ . To utrudni rozwiązanie zadania.
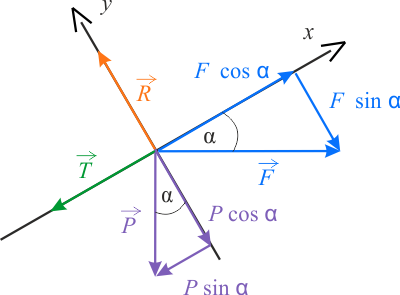
Obrócenie układu współrzędnych tak, aby siła

$\vec{R}$ była równoległa do osi

$OY$ , a

$\vec{T}$ do osi

$OX$ powoduje, że nie trzeba ich rozkładać na składowe. Skutkiem tego, nieznane siły nie pojawią się w obu wzorach jednocześnie, co ułatwi rozwiązanie zadania.

Rozwiązanie

Z wiemy, że w celu uzyskania stałej prędkości skrzyni, siły na nią działające muszą być w równowadze. Wobec tego równania równowagi dla układu będą wyglądały następująco: $\eqalign{ \sum F_x &= F \cos\alpha - P \sin\alpha - T = 0 \\ \sum F_y &= R - F \sin\alpha - P \cos\alpha = 0 }$ jest zależna od nacisku skrzyni na powierzchnię rampy i wynosi $T=\mu N$ , gdzie $N$ oznacza siłę nacisku. Z wiemy, że siła reakcji $R$ jest, co do wartości, równa sile nacisku $N$ , czyli $R=N$ . Można więc zapisać, że $T=\mu R$ . Uwzględniając ten fakt oraz zależność $P=mg$ w układzie równań, uzyskujemy: $\eqalign{ \sum F_x &= F \cos\alpha - mg\ \sin\alpha - \mu R = 0 \\ \sum F_y &= R - F \sin\alpha - mg\ \cos\alpha = 0 }$ W powyższych dwóch równaniach mamy dwie niewiadome ( $F$ i $R$ ), więc układ równań jest rozwiązywalny.

Przekształcając drugie równanie uzyskujemy wzór na siłę reakcji: $R = mg\ \cos\alpha + F \sin\alpha$ który po podstawieniu do pierwszego równania z układu i przekształceniu, pozwala wyznaczyć wzór na siłę pchającą skrzynię.
$F=mg \frac{\operatorname{tg}{\alpha}+\mu}{1-\mu \operatorname{tg}{\alpha}}$
Podstawiając dane obliczamy wartość siły: $\eqalign{F &=50 \cdot 10 \cdot \frac{\operatorname{tg}{30^{\circ}}+0,2}{1-0,2 \cdot \operatorname{tg}{30^{\circ}}} \begin{bmatrix} \mathrm{kg \frac{m}{s^2}} \end{bmatrix} = \\ &= 500 \cdot \frac{\frac{\sqrt{3}}{3}+0,2}{1-0,2 \cdot \frac{\sqrt{3}}{3}} \begin{bmatrix} \mathrm{N} \end{bmatrix}\approx 439\ \mathrm{N} }$

$F\approx439\,\mathrm{N}$

Odpowiedź

Aby skrzynia poruszała się ze stałą prędkością $\displaystyle{0,1\ \mathrm{\frac{m}{s}}}$ , wartość, działającej poziomo siły pchającej ją, powinna wynosić $439\ \mathrm{N}$ .

Wstęp

1. Wektory

2. Kinematyka

3. Zasady dynamiki

4. Praca, moc, energia, pęd

5. Dynamika układu punktów

6. Drgania i fale

7. Elektryczność

Ankieta