Zadanie 3.1.1.5
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.1. Zastosowanie I zasady Newtona
  4. 3.1.1 Nauka
  5. Zadanie 3.1.1.5

 Zadanie 3.1.1.5

Równia pochyła
Ciało o masie \(m\) jest wciągane, przy użyciu sznurka, po równi pochyłej pod kątem \(\alpha\) do podłoża. Pod jakim kątem, w stosunku do powierzchni równi, należy nachylić sznurek, aby jego naciąg był jak najmniejszy. Zakładamy, że ciało porusza się ruchem jednostajnym, a współczynnik tarcia kinetycznego wynosi \(\mu\).

 Wskazówka teoretyczna

 Zasady dynamiki Newtona
I zasada dynamiki

W inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.
Zgodnie z  I zasadą dynamiki, suma sił działających na układ musi wynosić zero.

II zasada dynamiki

Jeśli siły działające na ciało nie równoważą się, to ciało porusza się z przyspieszeniem wprost proporcjonalnym do siły wypadkowej, a odwrotnie proporcjonalnym do masy ciała. \[ \vec{a} = \frac{ \sum \vec{F}_{w} } {m} \left[ \frac{m}{s^2} = \frac{N}{kg} \right] \]
III zasada dynamiki

Jeśli ciało \(A\) działa na ciało \(B\) pewną siłą (siłą akcji), to ciało \(B\) działa na ciało \(A\) siłą (siłą reakcji) o takiej samej wartości i kierunku, lecz przeciwnym zwrocie. \[ \vec{F}_{AB} = -\vec{F}_{BA} \]

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa ciała \(m\),
- kąt nachylenia równi \(\alpha\),
- współczynnik tarcia kinetycznego \(\mu\),
- przyspieszenie ziemskie \(g\).

Szukane:
- kąt nachylenia sznurka, w stosunku do powierzchni równi, w momencie najmniejszego jego naciągu \(\beta\).

Analiza sytuacji

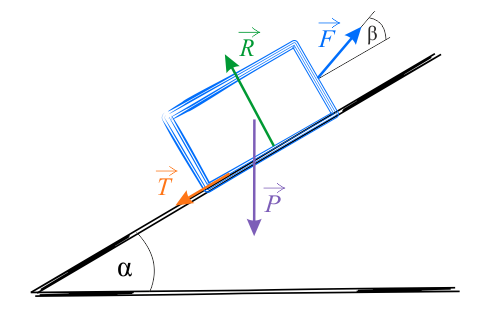
Rysunek


Na skrzynię, ciągniętą po rampie, działają następujące siły:
  • siła ciężkości \(\vec{P}\), skierowana pionowo w dół i o wartości \(mg\),
  • siła reakcji \(\vec{R}\), skierowana do góry w kierunku prostopadłym do rampy,
  • siła wynikająca z tarcia kinetycznego \(\vec{T}\), działająca wzdłuż rampy w kierunku przeciwnym do kierunku prędkości,
  • siła ciągnąca \(\vec{F}\), skierowana pod kątem \(\beta\) do płaszczyzny równi.
Poniżej znajduje się rysunek z siłami działającymi na skrzynię. Układ współrzędnych został obrócony w celu uproszczeniu równań.

W zadaniach tego typu, dla ułatwienia obliczeń, najczęściej siły rozdziela się na dwie grupy: działające wzdłuż osi \(OX\) oraz wzdłuż osi \(OY\). Gdyby układ współrzędnych był ustawiony standardowo (oś \(x\) poziomo, oś \(y\) pionowo), to z diagramu widać, że siły \(\vec{R}\) i \(\vec{T}\) należy rozbić na składowe. \[ \eqalign{ T_x &= T \cos\alpha \\ T_y &= T \sin\alpha \\ R_x &= R \sin\alpha \\ R_y &= R \cos\alpha } \] Oznacza to, że nieznane siły \(T_x\), \(T_y\), \(R_x\) i \(R_y\) pojawią się w obu wzorach: na sumę sił w osi \(OX\) oraz sumę sił w osi \(OY\). To utrudni rozwiązanie zadania.
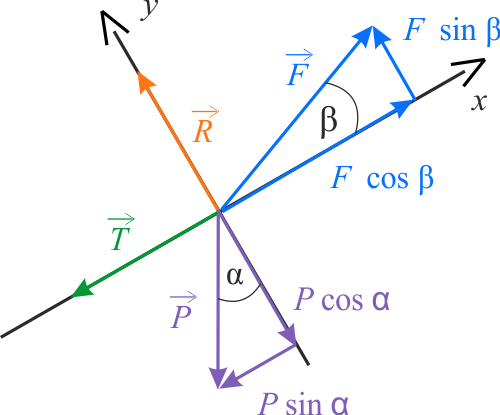
Obrócenie układu współrzędnych tak, aby siła \(\vec{R}\) była równoległa do osi \(OY\), a \(\vec{T}\) do osi \(OX\) powoduje, że nie trzeba ich rozkładać na składowe. Skutkiem tego, nieznane siły nie pojawią się w obu wzorach jednocześnie, co ułatwi rozwiązanie zadania.
Działające siły umieszczone w układzie współrzędnych

Rozwiązanie - krok 1

Z I zasady dynamiki Newtona wiemy, że w celu uzyskania stałej prędkości skrzyni, siły na nią działające muszą być w równowadze. Wobec tego równania równowagi dla układu będą wyglądały następująco: \[ \eqalign{ \sum F_x &= F \cos\beta - P \sin\alpha - T = 0 \\ \sum F_y &= R + F \sin\beta - P \cos\alpha = 0 } \] Siła tarcia kinetycznego jest zależna od nacisku skrzyni na powierzchnię rampy i wynosi \(T=\mu N\), gdzie \(N\) oznacza siłę nacisku. Z III zasady dynamiki wiemy, że siła reakcji \(R\) jest, co do wartości, równa sile nacisku \(N\), czyli \(R=N\). Można więc zapisać, że \(T=\mu R\). Uwzględniając ten fakt oraz zależność \(P=mg\) w układzie równań uzyskujemy: \[ \eqalign{ F \cos\beta - mg\,\sin\alpha - \mu R = 0 \\ R + F \sin\beta - mg\ \cos\alpha = 0 } \] W powyższych dwóch równaniach mamy dwie niewiadome (\(F\) i \(R\)), więc układ równań jest rozwiązywalny.

Przekształcając drugie równanie, uzyskujemy wzór na siłę reakcji: \[ R = mg\ \cos\alpha - F \sin\beta \]
Teraz siłę reakcji podstawiamy do równania pierwszego i otrzymujemy \[F\cos\beta-mg\sin\alpha-\mu (mg\cos\alpha-F\sin\beta)=0\]
Otrzymane równanie przekształćmy w taki sposób, aby otrzymać zależność \(F(\beta)\).
 \[F\cos\beta-mg\sin\alpha-\mu\,mg\cos\alpha+\mu\,F\sin\beta=0\] \[ F\left (\cos\beta+\mu\sin\beta \right )= mg\sin\alpha+\mu\,mg\cos\alpha \] 

\(\displaystyle{F(\beta)=\frac{mg\left (\sin\alpha+\mu\cos\alpha \right )}{\cos\beta+\mu\sin\beta} }\)

Rozwiązanie - krok 2

Wyznaczenie najmniejszego naciągu, wymaga obliczenia pochodnej z funkcji określającej siłę naciągu i przyrównanie jej do zera. W celu ułatwienia liczenia pochodnej, zapiszmy otrzymany wzór w postaci:

\(\displaystyle{F(\beta)=mg\left (\sin\alpha+\mu\cos\alpha \right )\cdot \left (\cos\beta+\mu\sin\beta \right )^{-1} }\)
 \[(\sin x)'=\cos x\]\[(\cos x)'=-\sin x\]\[\displaystyle{(a\,x^{\alpha})'=\alpha\cdot a\,x^{\alpha-1} }\] 
\(\displaystyle{\frac{\mathrm{d}F(\beta) }{\mathrm{d} \beta}=-mg\left (\sin\alpha+\mu\cos\alpha \right )\cdot \left ( -\sin\beta+\mu\cos\beta \right )\cdot \left (\cos\beta+\mu\sin\beta \right )^{-2} }\)
Otrzymaliśmy zależność
\(\displaystyle{\frac{\mathrm{d}F(\beta) }{\mathrm{d} \beta}=-mg\left (\sin\alpha+\mu\cos\alpha \right )\frac{\left ( -\sin\beta+\mu\cos\beta \right )}{\left (\cos\beta+\mu\sin\beta \right )^2} }\)

Rozwiązanie - krok 3

Kolejnym krokiem jest wyznaczenie, dla jakiego kąta \(\beta\), otrzymane równanie, przyjmuje wartość zero.

\(\displaystyle{-mg\left (\sin\alpha+\mu\cos\alpha \right )\frac{\left (-\sin\beta+\mu\cos\beta \right )}{\left (\cos\beta+\mu\sin\beta \right )^2}=0 }\)
Równanie to przyjmuje wartość zero wtedy, gdy
\(-\sin\beta+\mu\cos\beta=0\)
 Z warunków zadania wiemy, że wartości kątów \(\alpha\) i \(\beta\) zawierają się w przedziale \((0,\,90^{\circ})\), więc wartości funkcji trygonometrycznych tych kątów będą dodatnie. Współczynnik tarcia również jest dodatni, więc \(\sin\alpha+\mu\cos\alpha \neq0\). Wyrażenie \(\cos\beta+\mu\sin\beta\) jest podniesione do kwadratu, co za tym idzie, również jest dodatnie. 
Pochodna funkcji \(F(\beta)\) przyjmuje wartość zerową dla
\(\mu\cos\beta=\sin\beta\)
\(\displaystyle{\mu=\frac{\sin\beta}{\cos\beta}=\operatorname{tg}{\beta} }\)

Siła ciągnąca będzie miała najmniejszą wartość, gdy \(\displaystyle{\mu=\operatorname{tg}{\beta} }\).

Odpowiedź

Siła ciągnąca będzie miała najmniejszą wartość, gdy \(\displaystyle{\mu=\operatorname{tg}{\beta} }\).

Informacja

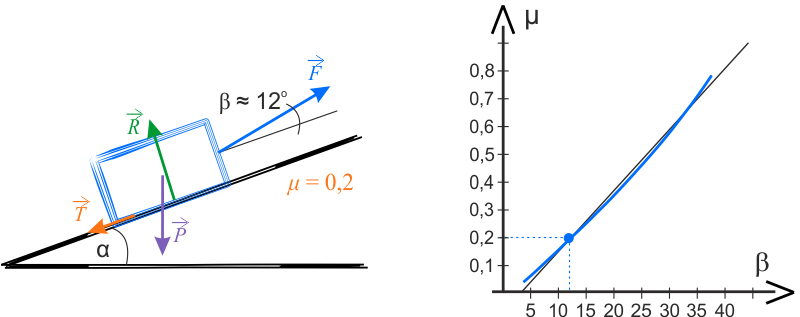
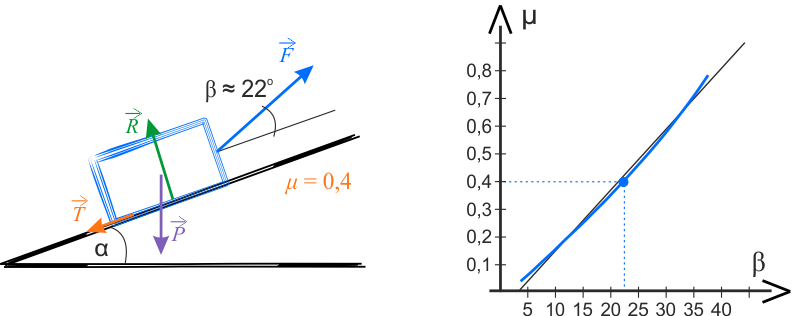
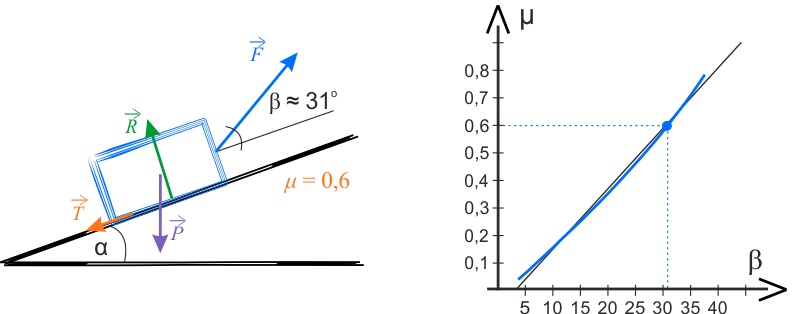
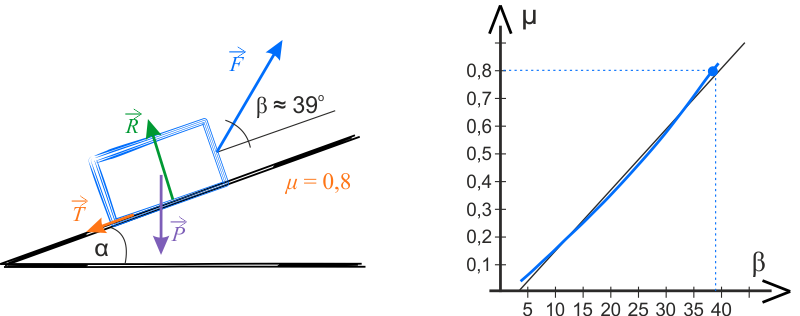
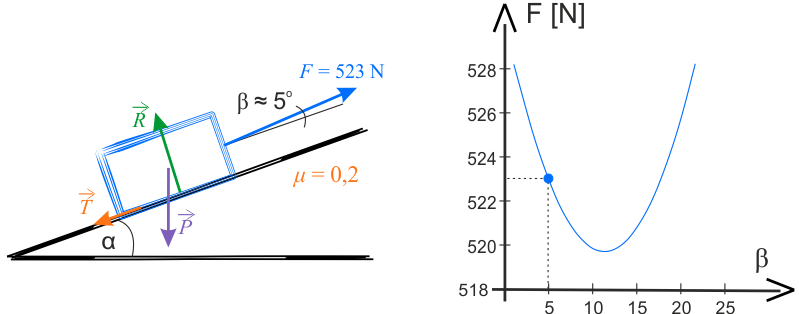
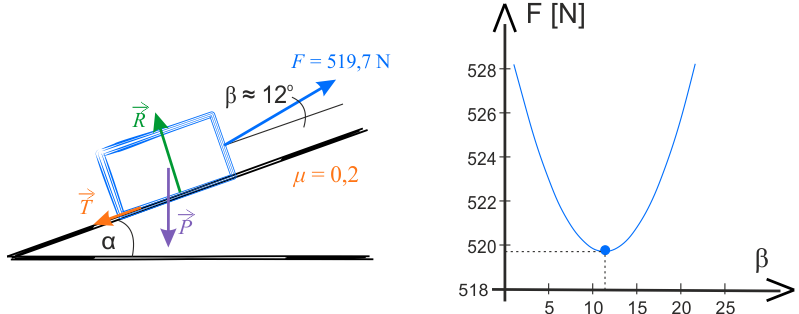
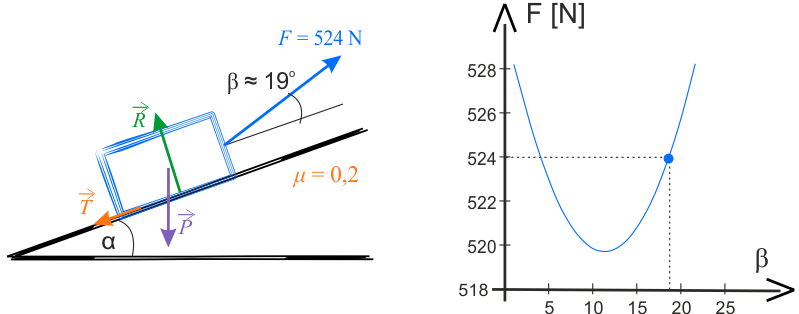
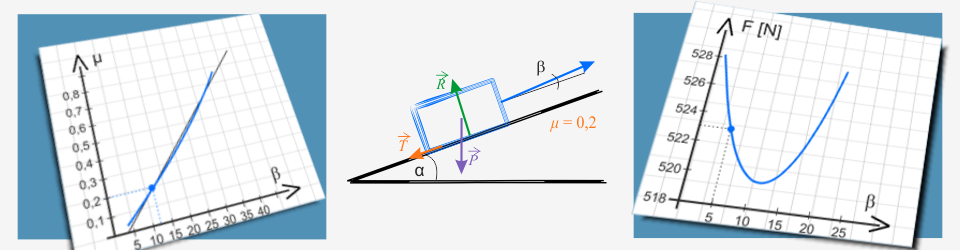
Pod rysunkami znajdują się strzałki. Po wciśnięciu szarego przycisku ze strzałką zobaczysz następne wykresy.

Poniżej pokazano, jak zmienia się kąt nachylenia sznurka, w stosunku do powierzchni równi, dla różnych współczynników tarcia kinetycznego. Dla każdego współczynnika tarcia kinetycznego wyznaczony jest kąt \(\beta\), przy którym siła naciągu sznura jest najmniejsza.

Na wykresie poniżej przedstawiono zależność \(\mu(\beta)=\operatorname{tg}{\beta}\) (niebieska krzywa) oraz ilustrację graficzną, prezentującą sposób nachylenia sznura.
Na wykresie znajduje się również linia prosta, służąca do przedstawienia krzywizny analizowanej funkcji.
Poniżej pokazano, jak zmienia się wartość siły naciągu nici, przy zmianach kąta nachylenia sznurka, podczas ciągnięcia ciała po tym samym podłożu. Obliczenia wykonano dla następujących wielkości: \(m=100\,\mathrm{kg}\) oraz \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\), kąt nachylenia równi \(\alpha=20^{\circ}\).