Zadanie 3.1.2.1
Informacja
Możesz zobaczyć odpowiedź, klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
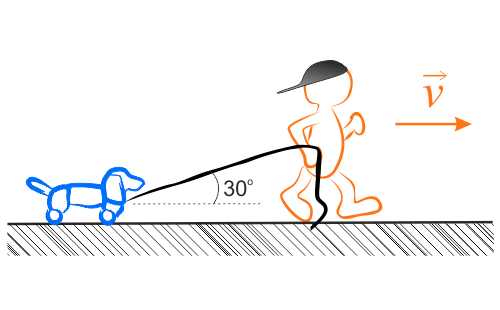
- masa zabawki \(m=1 \ \mathrm{kg}\),
- kąt pomiędzy linką a podłożem \(\alpha=30^{\circ}\),
- prędkość przesuwania się zabawki \(\displaystyle{v=3 \ \mathrm{\frac{m}{s}}}\),
- współczynnik tarcia między zabawką a asfaltem \(f=0,3\).
Szukane:
- siła, z jaką chłopiec działa na zabawkę \(F\).
Odpowiedź
Siła \(F\), z jaką chłopiec ciągnie zabawkę, ma wartość \(2,95 \,\mathrm{N}\). Jest to jednocześnie wartość siły naprężenia linki.
Polecenie
Z treści zadania wynika, że klocek porusza się ze stałą prędkością. Znając tę informację zastanów się, które z zasad dynamiki Newtona mogą być przydatne w rozwiązaniu tego zadania. Wybierz zasady, które uważasz za prawidłowe.
I zasada dynamiki
Jeżeli na ciało nie działa żadna siła lub siły działające równoważą się to ciało to pozostaje w spoczynku lub porusza się ruchem jednostajnie prostoliniowym.
II zasada dynamiki
Jeżeli na ciało działa siła niezrównoważona to ciało to porusza się ruchem zmiennym, a wartość przyspieszenia w tym ruchu jest wprost proporcjonalna do masy ciała i do wartości liczbowej działającej siły.
Jeśli ciało \(A\) działa na ciało \(B\) pewną siłą (siłą akcji), to ciało \(B\) działa na ciało \(A\) siłą (siłą reakcji) o takiej samej wartości i kierunku, lecz przeciwnym zwrocie.
Polecenie
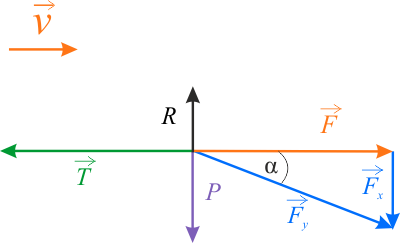
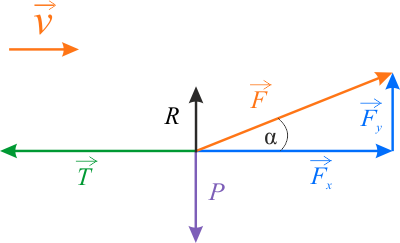
Narysuj diagram sił dla sytuacji z zadania. Wybierz jedną prawidłową odpowiedź, wśród dwóch przedstawionych poniżej.
Rozwiązanie
Po sporządzeniu diagramu sił działających w układzie możemy, korzystając z I zasady dynamiki Newtona, zapisać równanie wektorowej równowagi sił: \[ \vec{P} + \vec{R} + \vec{T} + \vec{F} = 0 \] Z tego wzoru, po przekształceniach, uzyskujemy równoważny układ dwóch równań w postaci skalarnej: \[ F_x - T = 0 \\ R + F_y - P = 0 \]
Podstawiając składowe siły naprężenia linki \(\vec{F}\) (równoległą i prostopadłą do osi układu współrzędnych) \[ F_x = F \cos \alpha \\ F_y = F \sin \alpha \] oraz zależności opisujące pozostałe siły \[ P = mg \\ R = N \\ T = f N \Rightarrow T = f R \] do równań w postaci wektorowej, uzyskamy układ równań w postaci skalarnej: \[F\cos \alpha - f R =0 \\ R + F \sin \alpha - mg = 0 \]
Polecenie
Na podstawie poniższego układu równań oblicz wartość siły naprężenia linki \(F\). Wybierz jedna prawidłową odpowiedź, wśród czterech przedstawionych poniżej.
\[\left\{\begin{matrix}F\cos \alpha-f R &=0 \\ R+F \sin\alpha-mg &=0 \end{matrix}\right.\]
\(F=2,95\,\mathrm{N}\)
Rozwiązanie
W utworzonym na podstawie diagramu sił układzie równań mamy dwie niewiadome: siłę naprężenia linki \(F\) oraz siłę reakcji podłoża \(R\). Dokonując prostego przekształcenia drugiego równania uzyskujemy wzór na wartość siły \(R\) \[ R = mg - F \sin \alpha \] który podstawiony do równania pierwszego, pozwala na uzyskanie szukanego wzoru na wartość siły \(F\)
\[ \eqalign{ F \cos \alpha - f R &= 0 \\ F \cos \alpha - f(mg - F \sin \alpha) &= 0 \\ F \cos \alpha - fmg + f F \sin \alpha &= 0 \\ F (\cos \alpha + f \sin \alpha) &= fmg } \\ \\ F = \frac{fmg}{\cos \alpha + f \sin \alpha} \]
Wartość siły wynosi:
\[\displaystyle{F= \frac{fmg}{\cos \alpha+f \sin \alpha}= \frac{0,3\cdot 1\cdot 10}{\frac{\sqrt{3}}{2}+0,3 \cdot \frac{1}{2}}= \frac{3}{0,866+0,15} \approx 2,95\,\mathrm{N}} \]
W żadnym z wzorów, przewijających się przy rozwiązywaniu zadania, nie pojawiała się prędkość przesuwania zabawki. Oznacza to, że nie ma ona żadnego wpływu na siłę naprężenia w lince, czyli siłę, z jaką chłopiec ciągnie zabawkę. Mimo to, informacja o prędkości w treści zadania, jest istotna. Dzięki wyraźnemu określeniu, że zabawka przesuwa się ze stałą prędkością, można było w trakcie rozwiązywania zadania, skorzystać z I zasady dynamiki Newtona.
Odpowiedź
Siła \(F\), z jaką chłopiec ciągnie zabawkę, ma wartość \(2,95 \,\mathrm{N}\). Jest to jednocześnie wartość siły naprężenia linki.