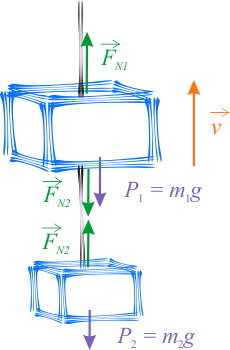Zadanie 3.1.2.2
Informacja
Możesz zobaczyć odpowiedź, klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- masa klocka zawieszonego wyżej \(m_1 =2\,\mathrm{kg} \),
- masa klocka zawieszonego niżej \(m_2 =1\,\mathrm{kg} \),
- prędkość podnoszenia klocków \(\displaystyle{v=3 \,\mathrm{\frac{m}{s}}}\).
Szukane:
- siła naprężenia sznurka łączącego klocki \(\vec{F}_{N2}\).
Odpowiedź
Siła naprężenia sznura łączącego oba klocki wynosi \(10 \,\mathrm{N}\).
Polecenie
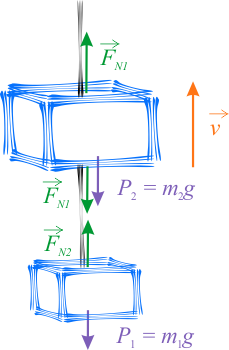
Wybierz jeden prawidłowy rysunek wśród dwóch przedstawionych poniżej.
Polecenie
Na podstawie rysunków napisz układ równań opisujących działanie sił. Wybierz jeden prawidłowy układ równań z czterech przedstawionych poniżej.
\(\left\{\begin{matrix}\vec{F}_{N1}-\vec{P}_1-\vec{P}_{2}=0\\ \vec{F}_{N2}=0\end{matrix}\right.\)
\(\left\{\begin{matrix}\vec{F}_{N1}-\vec{P}_1-\vec{F}_{N2}=0\\ \vec{F}_{N2}-\vec{P}_2=0\end{matrix}\right.\)
Rozwiązanie
Na dolny klocek działają dwie siły: skierowana w dół siła ciężkości \(\vec{P}_2\) o wartości \(m_2 g\) oraz skierowana w górę siła naprężenia sznura łączącego klocki \(\vec{F}_{N2}\). Natomiast na górny klocek działają trzy siły: skierowana w dół siła ciężkości \(\vec{P}_1\) o wartości \(m_1 g\), skierowana w dół siła naprężenia sznura łączącego klocki \(\vec{F}_{N2}\) oraz skierowana w górę siła naprężenia sznura, na którym zawieszony jest cały układ \(\vec{F}_{N1}\).
Na podstawie powyższych rozważań możemy zapisać równania opisujące działanie sił dla każdego klocka osobno.
Gdybyśmy zapisali tylko jedno równanie w formie skalarnej dla całego układu: \[\vec{F}_{N1}-\vec{P}_1-\vec{F}_{N2}+\vec{F}_{N2}-\vec{P}_2=0\] to byłoby ono wprawdzie poprawne, ale nieprzydatne w naszym zadaniu. Mamy obliczyć siłę naprężenia w \(\vec{F}_{N2}\) w sznurze łączącym klocki, a ta właśnie siła redukuje się z równania w trakcie rozwiązywania. \[\vec{F}_{N1}-\vec{P}_1-\vec{P}_2=0\] Dlatego lepiej zapisać dwa równania – po jednym dla każdego klocka.
Rozwiązanie
Na podstawie powyższych rozważań możemy zapisać równania, opisujące działanie sił dla każdego klocka osobno.
W tym momencie można zauważyć jedną ważną rzecz – równanie dla pierwszego klocka nie jest nam w ogóle potrzebne! W drugim równaniu mamy tylko dwie siły: szukaną \(\vec{F}_{N2}\) oraz znaną \(\vec{P}_2\). Czyli, żeby obliczyć wartość siły naprężenia w sznurze łączącym oba klocki, nie potrzebujemy informacji o górnym klocku i działających na niego siłach.
Pamiętając, że wartość siły ciężkości działającej na niższy klocek ma wartość \(P_2=m_2g\) otrzymujemy: \[ \eqalign{ \vec{F}_{N2} - \vec{P}_2 &= 0 \\ F_{N2} - m_2g &= 0 \\ F_{N2} &= m_2g =1 \cdot 10=10\,\mathrm{N} } \]
Naprężenie sznurka łączącego oba klocki, nie zależy ani od masy górnego klocka, ani od prędkości, z jaką się one poruszają. Naprężenie sznurka miałoby taką samą wartość, gdyby górnego klocka nie było, lub gdyby klocki nie poruszały się.