Zadanie 3.2.1.1
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.2. Stała siła
  4. 3.2.1 Nauka
  5. Zadanie 3.2.1.1

 Zadanie 3.2.1.1

Układ trzech sił
Mamy układ trzech ciał \(A\), \(B\) i \(C\), które działają na siebie za pośrednictwem nieważkiego sznura. Ciało \(A\) ma masę \(2 \ \mathrm{kg}\) i działa na ciała \(B\) oraz \(C\) odpowiednio siłami \(\vec{F}_{AB}=2\vec{i}-3\vec{j} \ \mathrm{[N]}\) i \(\vec{F}_{AC} = \vec{i} - \vec{j} \ \mathrm{[N]}\). Z jakim przyspieszeniem porusza się ciało \(A\)? Jaka jest wartość tego przyspieszenia?

 Wskazówka teoretyczna

 Teoria - zasady dynamiki Newtona
I zasada dynamiki

W inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.
Zgodnie z  I zasadą dynamiki, suma sił działających na układ musi wynosić zero.

II zasada dynamiki

Jeśli siły działające na ciało nie równoważą się, to ciało porusza się z przyspieszeniem wprost proporcjonalnym do siły wypadkowej, a odwrotnie proporcjonalnym do masy ciała. \[ \vec{a} = \frac{ \sum \vec{F}_{w} } {m} \left[ \frac{m}{s^2} = \frac{N}{kg} \right] \]
III zasada dynamiki

Jeśli ciało \(A\) działa na ciało \(B\) pewną siłą (siłą akcji), to ciało \(B\) działa na ciało \(A\) siłą (siłą reakcji) o takiej samej wartości i kierunku, lecz przeciwnym zwrocie. \[ \vec{F}_{AB} = -\vec{F}_{BA} \]

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa ciała \(A\): \(m_A = 2 \ \mathrm{kg}\),
- siła, z jaką ciało \(A\) działo na ciało \(B\): \(\vec{F}_{AB}=2\vec{i}-3\vec{j} \ \mathrm{[N]}\),
- siła, z jaką ciało \(A\) działo na ciało \(C\): \(\vec{F}_{AC} = \vec{i} - \vec{j} \ \mathrm{[N]}\).

Szukane:
- wektor przyspieszenie ciał \(A\): \(\vec{a}\),
- wartość przyspieszenia ciała \(A\): \(a\).

Rysunek
II zasada dynamiki - 
Jeżeli na ciało o masie \(m\) zadziała siła \(\vec{F}\) (lub wypadkowa kilku sił działających na ciało wynosi \(\vec{F}\)), to ciało to będzie poruszać się z przyspieszeniem \(\vec{a}\), proporcjonalnym do działającej siły. Współczynnikiem proporcjonalności jest odwrotność masy ciała, na które działa siła:

\(\displaystyle{\vec{a}=\frac{1}{m}\vec{F}}\)

Ponieważ masa \(m\) jest skalarem, to kierunki siły i przyspieszenia są takie same. Powyższe równanie, które jest równaniem wektorowym można także zapisać, jako układ trzech równań skalarnych. W kartezjańskim układzie współrzędnych mamy:

\(\displaystyle{a_x=\frac{F_x}{m}}\),     \(\displaystyle{a_y=\frac{F_y}{m}}\),     \(\displaystyle{a_z=\frac{F_z}{m}}\)

Komentarz: W zadaniach często będziemy mieli do czynienia z przypadkiem, gdy na ciało działa siła, której kierunek działania nie będzie ulegał zmianie w czasie trwania ruchu. Wtedy wygodnie jest wybrać kierunek osi \(x\) zgodnie z kierunkiem wektora działającej siły. Przy takim wyborze osi pozostałe składowe wektora siły będą równe zero, zatem niezerową wartość przyspieszenia będzie miała składowa \(a_x\). Pozostałe składowe przyspieszenia, zgodnie z powyższymi równaniami, będą miały wartość równą zero. Można wtedy opuścić wskaźnik \(x\) otrzymując drugą zasadę dynamiki w postaci:

\(\displaystyle{a=\frac{F}{m}}\)

gdzie \(a\) i \(F\) są wartościami odpowiednich wektorów. Mogą one być zarówno dodatnie jak i ujemne.

Analiza sytuacji

Podczas analizy sytuacji z zadania potrzebna jest znajomość dwóch zasad dynamiki: II oraz III zasady dynamiki Newtona.
 Skoro w zadaniu szukamy przyspieszenia działającego na ciało \(A\) i wiemy, że przyspieszenie jest wywoływane jakąś niezrównoważoną siłą, to druga zasada dynamiki podaje nam prosty wzór na określenie zależności między tą siłą a przyspieszeniem. 

Na podstawie II zasady dynamiki Newtona możemy napisać, że przyspieszenie ciała o masie \(m\) jest równe:

\(\displaystyle{ \vec{a} = \frac{\vec{F}}{m}} \)
gdzie \(\vec{F}\) jest wypadkową sił działających na ciało.

 Ciała są połączone ze sobą sznurkiem, w związku z czym, jeśli ciało \(A\) działa na ciała \(B\) i \(C\) jakimiś siłami, to zgodnie z III zasadą dynamiki możemy oczekiwać, że ciała \(B\) i \(C\) działają także na ciało \(A\) identycznymi, lecz przeciwnie skierowanymi siłami.  
Korzystając z III zasadą dynamiki Newtona można przyjąć zależności \[ \vec{F}_{BA} = - \vec{F}_{AB} \\ \vec{F}_{CA} = - \vec{F}_{AC} \]
Dzięki tym zależnością określimy siłę wypadkową jako \[ \vec{F} = \vec{F}_{BA} + \vec{F}_{CA} = (-\vec{F}_{AB}) + (-\vec{F}_{AC}) \] Ostatecznie uzyskujemy wzór na przyspieszenie
\( \displaystyle{\vec{a} = \frac{\vec{F}}{m} = \frac{(-\vec{F}_{AB}) + (-\vec{F}_{AC})}{m}} \)
\( \displaystyle{\vec{a} =- \frac{\vec{F}_{AB}+\vec{F}_{AC}}{m}} \)

Rozwiązanie

Podstawiając wartości liczbowe do wzoru rozwiązujemy równanie:

\(\displaystyle{\vec{a}=-\frac{\vec{F}_{AB}+\vec{F}_{AC}}{m}=}\)
 \[ \eqalign{& =- \frac{(2\vec{i}-3\vec{j}) + (\vec{i} - \vec{j})}{2} \begin{bmatrix} \mathrm{\frac{N}{kg}} \end{bmatrix} = \\& = - \frac{3\vec{i} - 4\vec{j}}{2} \begin{bmatrix} \mathrm {\frac{\frac{\cancel{kg}m}{s^2}}{\cancel{kg}}} \end{bmatrix} = \\& = -(1,5 \vec{i} - 2 \vec{j}) \begin{bmatrix} \mathrm{\frac{m}{s^2}}\end{bmatrix} = } \]  
\(\displaystyle{=( -1,5 \vec{i} + 2\vec{j}) \,\mathrm{\frac{m}{s^2}} } \)

Wartość przyspieszenia uzyskujemy obliczając długość wektora przyspieszenia:
\[a =\sqrt{1,5^2+2^2} = 2,5 \ \mathrm{\frac{m}{s^2}}\]

Rozwiązanie graficzne

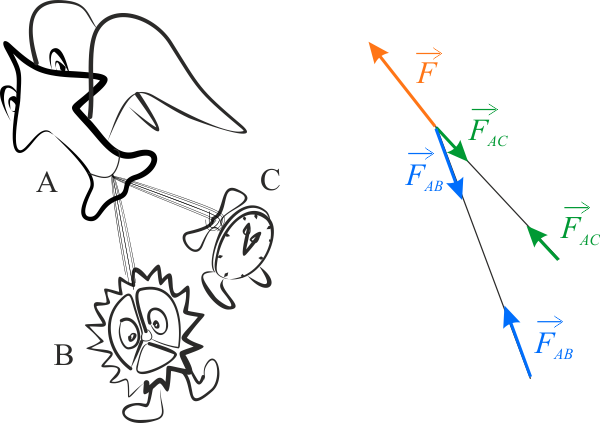
Rozwiązanie można zilustrować metodą graficzną. W tym celu utworzymy diagram sił. Przy jego tworzeniu ważne jest zachowanie właściwych miar kątów oraz odpowiedniej skali dla długości wektorów sił.

Schemat postępowania pokazano na wykresie poniżej.
1. Narysowanie wektora \(\vec{F}_{AB}\).
2. Narysowanie wektora \(\vec{F}_{AC}\).
3. Wykonanie dodawania wektorów \(\vec{F}_{CB}=\vec{F}_{AB}+\vec{F}_{AC}\).
4. Narysowanie wektora przeciwnego do wektora \(\vec{F}=-\vec{F}_{CB}\).
5. Przesunięcie wektora \(\vec{F}\) do początku układu współrzędnych i odczytanie jego współrzędnych \(\vec{F}=-3\hat{i}+4\hat{j}\,[\mathrm{N}\).

Odczytane współrzędne podstawiamy do wzoru i dalej postępujemy jak poprzednio.

\(\displaystyle{\vec{a}=-\frac{-3\hat{i}+4\hat{j}}{2}=}\)
\(\displaystyle{=( -1,5 \vec{i} + 2\vec{j}) \,\mathrm{\frac{m}{s^2}} } \)

Wartość przyspieszenia uzyskujemy obliczając długość wektora przyspieszenia:
\[a =\sqrt{1,5^2+2^2} = 2,5 \ \mathrm{\frac{m}{s^2}}\]

Odpowiedź

Przyspieszenie działające na ciało \(A\) jest wektorem \(\displaystyle{\vec{a}= (-1,5 \vec{i}+2\vec{j}) \ \mathrm{\frac{m}{s^2}}}\), a jego wartość wynosi \(\displaystyle{a=2,5 \ \mathrm{\frac{m}{s^2}}}\).