Zadanie 3.2.1.2
Wskazówka teoretyczna
\[v=v_0+at\]
\(v_0\) - wartość prędkości początkowej,
\(a\) - wartość przyspieszenia \(a=const\).
Droga \(S\) przebyta przez ciało w ruchu jednostajnie przyspieszonym po czasie \(t\):
\[\displaystyle{S=S_0+v_0t+\frac{1}{2}at^2}\]
\(S_0\) - droga początkowa w chwili \(t=0\),
\(v_0\) - wartość prędkości początkowej,
\(a\) - wartość przyspieszenia \(a=const\).
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- masa samochodu \(m=900\ \mathrm{kg}\),
- siła hamująca \(F=300\ \mathrm{N}\),
- prędkość początkowa samochodu \(\displaystyle{v_0=36\ \mathrm{\frac{km}{h}}=10\ \mathrm{\frac{m}{s}}}\).
Szukane:
- zależność prędkości od czasu \(v(t)\),
- czas hamowania \(t_h\),
- droga hamowania \(S_h\).
Analiza sytuacji
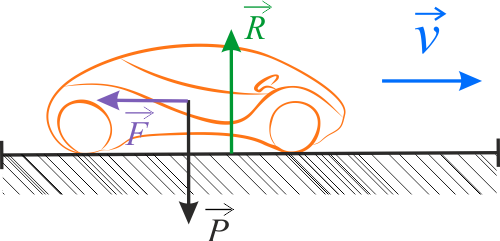
Po wyłączeniu silnika na samochód będą działały trzy siły: siła ciężkości \(\vec{P}\), siła reakcji \(\vec{R}\) oraz siła hamująca \(\vec{F}\). Siły te zaznaczone są na powyższym rysunku. Siła hamująca jest wypadkową wszystkich sił oporu ruchu (tarcia, oporów powietrza, itp.),
Z III zasady dynamiki Newtona wiemy, że siła reakcji \(\vec{R}\) będzie, co do wartości, równa sile ciężkości \(\vec{P}\), lecz skierowana w przeciwnym kierunku. Oznacza to, że przy braku innych sił działających w pionie, można je pominąć.
wobec czego możemy je pominąć przy układaniu równań opisujących układ. Pozostaje jednak, działająca w poziomie, w kierunku przeciwnym do wektora prędkości, niezrównoważona niczym, siła hamująca \(\vec{F}\). Pod działaniem tej siły samochód będzie poruszał się ruchem jednostajnie opóźnionym.
Skoro siły działające w pionie wzajemnie się redukują, to możemy, sytuację opisaną w zadaniu, przedstawić w jednoosiowym układzie współrzędnych. Korzystając z właściwości ruchu jednostajnie opóźnionego otrzymujemy wzory, które po dopasowaniu do oznaczeń z zadania, będą potrzebne do obliczenia szukanych wartości: \[ v_x=v_{0x} + a_x t_h \\ x = x_0 + v_{0x} t_h + \frac{a_x t_h^2}{2} \] Korzystając z II zasady dynamiki uzyskujemy wzór łączący zależnością siłę hamującą z wartością przyspieszenia: \[ a=\frac{F}{m} \\ \Downarrow \\ a_x=\frac{-F_x}{m} \] We wzorze pojawił się znak minus, gdyż zgodnie z przyjętym układem współrzędnych siła hamująca, a w konsekwencji i przyspieszenie pojazdu, działa przeciwnie do kierunku jego ruchu.
Rozwiązanie
\[ v_x=v_{0x} + a_x t_h \\ x = x_0 + v_{0x} t_h + \frac{a_x t_h^2}{2} \] Z odpowiednich przekształceń pierwszego wzoru
Czas hamowania \(t_h\) to czas, po którym samochód całkowicie się zatrzyma – możemy więc przyjąć, że prędkość \(v\) we wzorze ma wartość \(0\). Pozwala to przekształcić wzór następująco: \[ \eqalign{ v &= v_{0x} + a_x t_h \\ 0 &= v_{0x} + a_x t_h \\ - a_x t_h &= v_{0x} \\ t_h &= \frac{-v_{0x}}{ax} } \]
uzyskamy równanie na czas hamowania \(t_h\), w którym nieznaną wartością jest przyspieszenie \(a\).
Podstawiając do wzoru \(\displaystyle{a_x=\frac{-F_x}{m}}\) dane otrzymujemy wartość przyspieszenia: \(\displaystyle{a\approx -0,33\ \mathrm{\frac{m}{s^2}} } \)
\[ \eqalign{ a_x &= \frac{-F_x}{m}= \\ &= \frac{-300}{900} \begin{bmatrix} \mathrm{\frac{N}{kg}} \end{bmatrix} = \\ &= - \frac{1}{3} \begin{bmatrix} \mathrm{\frac{\cancel{kg}\frac{m}{s^2}}{\cancel{kg}}} \end{bmatrix} = \\ &\approx -0,33\ \mathrm{\frac{m}{s^2}} } \]
Wartość przyspieszenia podstawiamy do wzoru \(\displaystyle{t_h= \frac{-v_{0x}}{a_x}}\) i obliczamy czas hamowania \(t_h=30,3\ \mathrm{s}\).
\[ \eqalign{ t_h &= \frac{-v_{0x}}{a_x} = \\ &= \frac{-10}{-0,33} \begin{bmatrix} \mathrm{\frac{\frac{\cancel{m}}{\cancel{s}}}{\frac{\cancel{m}}{s^\cancel{2}}}} \end{bmatrix} = \\ &= 30,3\ \mathrm{s} } \]
Mając obliczony czas hamowania oraz przyspieszenie samochodu w jego trakcie, możemy obliczyć drogę hamowania:
Rozwiązanie
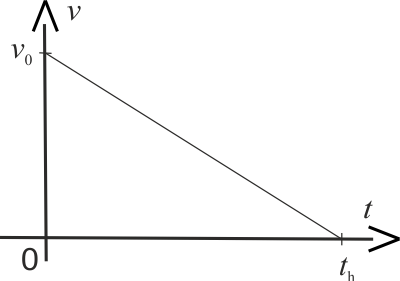
Wartość \(v_0\) jest podana w treści zadania. Należy jeszcze określić położenie punktu \(t_h\). Korzystając ze wzorów, opisujących ruch jednostajnie opóźnionym i
W ruchu jednostajnie opóźnionym prędkość opisana jest wzorem: \[ v=v_0-at \] Chcąc, na jego podstawie, obliczyć czas, po którym prędkość samochodu spadnie do \(0\ \mathrm{\frac{km}{h}}\), musimy go nieco zmodyfikować: \[ \eqalign{ 0 &= v_0 - at_h \\ at_h &= v_0 \\ t_h &= \frac{v_0}{a} } \]
je na potrzeby obliczenia czasu hamowania \(t_h\), otrzymujemy: \[ t_h=\frac{v_0}{a} \]
Do obliczenia szukanej wartości brakuje już tylko wartości przyspieszenia samochodu \(a\). Uzyskamy ją z przekształcając wzór z II zasady dynamiki \(\vec{F}= m\,\vec{a}\) i podstawiając dane:
Podstawiając obliczone przyspieszenie \(a\) do wzoru na czas hamowania, otrzymujemy \(t_h\): \[ \eqalign{ t_h &= \frac{v_0}{a} = \\ &= \frac{10}{0,33} \begin{bmatrix} \mathrm{\frac{\frac{\cancel{m}}{\cancel{s}}}{\frac{\cancel{m}}{s^{\cancel{2}}}}} \end{bmatrix} = \\ &=30,3\ \mathrm{s} } \]
Pozostało obliczyć drogę hamowania samochodu. Geometryczną miarą przebytej drogi jest pole pod krzywą, przedstawiającą zależność prędkości od czasu \(v(t)\).
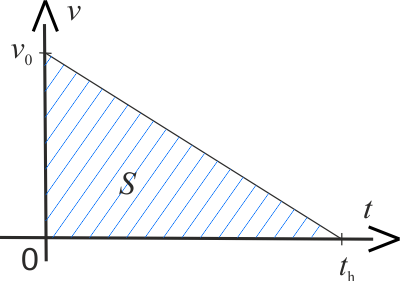
Korzystając ze wzoru na pole trójkąta i dostosowując go do oznaczeń na wykresie obliczamy: \[ \eqalign{ S &= \frac{1}{2} t_h v_0 = \\ &= \frac{1}{2} \cdot 30,3 \cdot 10 \begin{bmatrix} \mathrm{\cancel{s}\cdot\frac{m}{\cancel{s}}} \end{bmatrix} = \\ &= 151,5 \mathrm{m} } \]
Odpowiedź
Czas hamowania, liczony od momentu wyłączenia silnika do całkowitego zatrzymania pojazdu, wynosi \(t_h=30,3\ \mathrm{s}\), natomiast droga przebyta w tym czasie równa jest \(S=151,5\ \mathrm{m}\).
