Analiza sytuacji

Umieszczona w treści zadania informacja, o swobodnym spływaniu wody po uderzeniu w ścianę, jest wyraźnym sygnałem, że następuje wyhamowanie strumienia wody. Możemy więc uznać, że jest to ruch jednostajnie zmienny, wobec czego, przy rozwiązywaniu zadania, możemy użyć II zasady dynamiki. Na wodę działa również siła hamująca. III zasada dynamiki odpowiada na pytanie jaka to siła – siła reakcji ściany.

Zastosowanie II zasady dynamiki Newtona wymaga znajomości masy. Jednak w treści zadania nie ma podanej tej wielkości, dlatego też musimy uzupełnić zadanie o ten element.

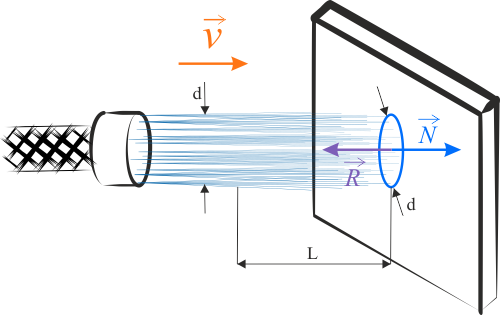
 Jak wprowadzić do zadania masę?  Zaznaczamy na rysunku odcinek strumienia wody o długości \(L\). Odcinek ten będzie posiadał masę, którą oznaczymy przez \(\Delta m\). Wszystkie cząsteczki wody zawarte w tym odcinku, poruszają się z prędkością \(v\) i dotrą do ściany w czasie \(\Delta t\). Wobec tego długość zaznaczonego odcinka można określić według wzoru \(L=v \Delta t\). 
 Masa wycinka strumienia  Biorąc pod uwagę, że zaznaczony wycinek jest walcem, możemy na podstawie długości \(L\) oraz pola przekroju \(\displaystyle{S=\pi \frac{d^2}{4}}\) obliczyć jego objętość \(v_{wody}\). Stąd już prosta droga do wyznaczenia masy wycinka strumienia, dzięki wykorzystaniu wzoru na gęstość \(\displaystyle{\rho=\frac{m}{v_{wody}}}\). Mamy więc: \[\rho=\frac{m}{v} \Rightarrow \Delta m = \rho\ v = \rho\ L\ s = \rho\ v\Delta t \frac{\pi d^2}{4} \]  
Masa wycinka wody wynosi \(\displaystyle{\Delta m=\rho\ v\Delta t \frac{\pi d^2}{4}}\)

Mamy już określoną masę zaznaczonego odcinka wody, więc, do zastosowania II zasady dynamiki Newtona, brakuje tylko określenia przyspieszenia strumienia wody \(a\). Wiemy, że po zderzeniu ze ścianą woda spływa po niej swobodnie. Oznacza to, że każda cząsteczka wody w wyniku zderzenia zostaje wyhamowana z prędkości \(v\) do \(0\). Korzystając z wzoru na przyspieszenie uzyskujemy: \[ a=\frac{\Delta v}{\Delta t} \Rightarrow a=\frac{0-v}{\Delta t} = - \frac{v}{\Delta t} \]
Z dotychczasowych rozważań otrzymaliśmy układ dwóch równań
\[ \left\{\begin{matrix} \Delta m =& \rho\ v\ \Delta t \frac{\Large{\pi d^2}}{\Large{4}}\\a =& - \frac{\Large{v}}{\Large{\Delta t}} \end{matrix}\right. \]

Rozwiązanie

Wykorzystując oba równania zgodnie z II zasady dynamiki Newtona, uzyskujemy:

 Przekształcenia  \[ \eqalign{-R &= a \Delta m \\& = - \frac{v}{\cancel{\Delta t}} \rho\ v\cancel{\Delta t} \frac{\pi d^2}{4} = \\& = -\rho v^2 \frac{\pi d^2}{4}} \]  
Ponieważ siła nacisku wody na ścianę jest, co do wartości, równa sile reakcji ściany \(R=F\), więc ostatecznie: \[ N = \rho v^2 \frac{\pi d^2}{4} \] Podstawiając dane obliczamy wartość siły: \[ \eqalign{ N &= \rho v^2 \frac{\pi d^2}{4} = \\& = 1000 \cdot 12^2 \cdot \frac{3,14 \cdot 0,05^2}{4} \begin{bmatrix} \mathrm{\frac{kg}{\cancel{m^3}}\cdot \frac{m^{\cancel 2}}{s^2} \cdot \cancel{m^2}} \end{bmatrix} = \\& \approx 283\ \mathrm{N} } \]