Zadanie 3.2.1.4
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.2. Stała siła
  4. 3.2.1 Nauka
  5. Zadanie 3.2.1.4

 Zadanie 3.2.1.4

Siła w ruchu po okręgu
Punkt materialny porusza się ze stałym przyspieszeniem kątowym \(\displaystyle{5\ \mathrm{\frac{rad}{s^2}}}\) po okręgu o promieniu \(0,5\ \mathrm{m}\). Po jakim czasie, liczonym od momentu rozpoczęcia ruchu, siła dośrodkowa będzie \(4\) razy większa od siły stycznej?

 Wskazówka teoretyczna

 Teoria - ruch po okręgu
Przyspieszenie w ruchu po okręgu:

\(\vec{a}=\vec{a}_s+\vec{a}_d\)
\(a_s=\varepsilon R\)
\(\displaystyle{\varepsilon=\frac{\mathrm{d}\omega}{\mathrm{d}t}=\frac{\mathrm{d}^2\varphi}{\mathrm{d}t^2}}\)
\(\displaystyle{a_d=\omega ^2 R=\frac{v^2}{R}}\)
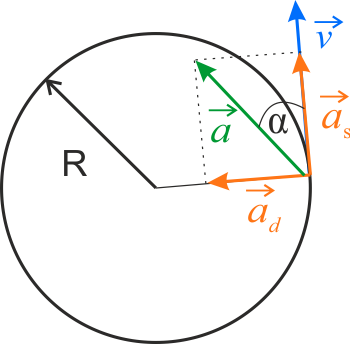
\(\displaystyle{\operatorname{tg}{\alpha}={\frac{a_d}{a_s}}}\)
\(\displaystyle{T=\frac{2\pi}{\omega}=\frac{1}{f}}\)
Rysunek

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- promień okręgu, po którym porusza się punkt \(R = 0,5 \ \mathrm{m}\),
- przyspieszenie kątowe punktu \(\displaystyle{ \varepsilon = 5\ \mathrm{\frac{rad}{s^2}}}\) ,
- zadany stosunek sił dośrodkowej i stycznej \(\displaystyle{\frac{F_d}{F_s} = 4}\).

Szukane:
- czas, po jakim wystąpi zadany stosunek sił \(t\).

Analiza sytuacji

Z treści zadania wiemy, że punkt materialny porusza się po okręgu. Musi więc na niego działać jakaś siła, powodująca zakrzywienie toru ruchu. Siłą tą jest siła dośrodkowa \(F_d\). Działanie tej siły powoduje ciągłą zmianę kierunku wektora prędkości \(\vec{v}\) punktu. Siła dośrodkowa działa wzdłuż promienia okręgu i nie powoduje zmiany wartości prędkości \(\vec{v}\) punktu materialnego.

Kolejna przydatna informacja, zawarta w treści, dotyczy przyspieszenia kątowego. Skoro punkt materialny porusza się ze stałym przyspieszeniem kątowym \(\varepsilon\) o wartości większej od \(0\), to musi istnieć także, powiązane z tym punktem, przyspieszenie styczne \(a_s\), również o wartości większej od \(0\). Zgodnie z II zasady dynamiki Newtona, przyspieszeniu takiemu towarzyszy jakaś niezrównoważona siła - w omawianym przypadku jest to siła styczna \(F_s \). Siła ta jest odpowiedzialna za nadanie punktowi materialnemu przyspieszenia stycznego \(a_s\) i powodująca zmianę wartości jego prędkości.

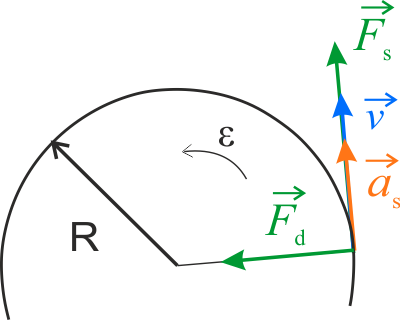
Rysunek

Podana wcześniej zależność, \(\displaystyle{\frac{F_d}{F_s} = 4}\), przedstawia stosunek wartości siły dośrodkowej do siły stycznej. Aby z niej skorzystać, musimy powiązać zmienne \(F_d\) i \(F_s\) ze znanymi wartościami z treści zadania.

Korzystając ze znanych wzorów  Przyłożona do punktu materialnego siła styczna, jest opisana II zasadą dynamiki jako \(F_s=ma_s\) gdzie \(m\) oznacza masę punktu materialnego, a \(a_s\) jego przyspieszenie styczne. Znając promień \(R\) okręgu, po którym porusza się punkt materialny oraz jego przyspieszenie kątowe \(\varepsilon\), możemy określić przyspieszenie styczne \(a_s=\varepsilon R\). Łącząc oba wzory uzyskujemy wyrażenie opisujące siłę styczną.  możemy określić wzór na siłę styczną: \[ F_s = m \varepsilon R \] 
Łącząc wzór na przyspieszenie kątowe z wzorem na siłę dośrodkową  Siła dośrodkowa jest opisana wzorem \(F_d=m\omega^2 R\), gdzie \(\omega\) oznacza prędkość kątową punktu materialnego. Z treści zadania wynika, że wartość przyspieszenia kątowego jest stała, niezmienna w czasie, wobec czego możemy zrezygnować z różniczkowania i zastosować wzór \(\displaystyle{\varepsilon=\frac{\omega}{t} }\). Przekształcając go do postaci \(\omega=\varepsilon t\) i używając we wzorze na siłę dośrodkową mamy:\[ F_d=m\omega^2 R=m (\varepsilon t)^2 R\]  , uzyskujemy: \[ F_d = m ( \varepsilon t )^2 R \] Podstawiając oba wzory uzyskujemy równanie: \[ \frac{F_d}{F_s} = \frac{m ( \varepsilon t )^2 R}{m \varepsilon R} \] 

Rozwiązanie

Rozwiązując powyższe równianie otrzymujemy:

\(\displaystyle{\frac{F_d}{F_s}=\varepsilon t^2}\)
 \[ \eqalign{ \frac{F_d}{F_s} &= \frac{\cancel{m} \omega^2 \cancel{R}}{\cancel{m} \varepsilon \cancel{R}} = \\& = \frac{(\varepsilon t)^2}{\varepsilon} = \\& = \frac{\varepsilon^{\cancel{2}}t^2}{\cancel{\varepsilon}} = \\& = \varepsilon t^2 } \]  

Po podstawieniu wartość stosunku sił \(\displaystyle{\frac{F_d}{F_s}=4}\) i przekształceniu dostajemy:
\(\displaystyle{t=\frac{2\sqrt{5}}{5}\approx0,894\,\mathrm{s}}\)
 \[ \eqalign{ \varepsilon t^2 &= \frac{F_d}{F_s} \\ \varepsilon t^2 &= 4 \\ t^2 &= \frac{4}{\varepsilon} \\ t &= \frac{2}{\sqrt{\varepsilon}} \\ t &= \frac{2}{\sqrt{5}}\ \mathrm{\begin{bmatrix} \frac{1}{\sqrt{\frac{1}{s^2}}} \end{bmatrix} } = \\& = 0,894\, \mathrm{s}} \] 

Odpowiedź

Czas \(t\), który minie od rozpoczęcia ruchu punktu materialnego do momentu, w którym stosunek siły dośrodkowej do siły stycznej osiągnie wartość \(\displaystyle{\frac{F_d}{F_s}=4}\), wynosi \(0,894\ \mathrm{s}\).