Zadanie 3.2.1.5
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.2. Stała siła
  4. 3.2.1 Nauka
  5. Zadanie 3.2.1.5

 Zadanie 3.2.1.5

Zmiana pędu
Kula o masie \(1\,\mathrm{kg}\) i prędkości \(\displaystyle{100\,\mathrm{\frac{m}{s}}}\) trafia prostopadle w betonową ścianę i odbija się od niej również prostopadle. Prędkość kuli po odbiciu wynosi  \(\displaystyle{50\,\mathrm{\frac{m}{s}}}\). Ile wynosi zmiana pędu kuli? Oblicz wartość średniej siły działającej na kulę, jeśli uderzenie trwało \(10^{-3}\,\mathrm{s}\).

 Wskazówka teoretyczna

 Teoria - II zasada dynamiki w postaci z pędem
II zasada dynamiki Newtona, sformułowana za pomocą pędu, w inercjalnym układzie odniesienia (masa jest stała), ma postać:
\[\displaystyle{\vec{F}_{wyp}=\frac{\mathrm{d} \vec{p}}{\mathrm{d} t}}\]
\[\displaystyle{\vec{F}_{wyp}=\frac{\mathrm{d} (m\,\vec{v})}{\mathrm{d} t}=m\frac{\mathrm{d} \vec{v}}{\mathrm{d} t}=m\,\vec{a}}\]

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa kulki \(m=1\ \mathrm{kg}\),
- wartość prędkości początkowej kuli \(\displaystyle{v_1=100\ \mathrm{\frac{m}{s}}}\),
- wartość prędkości kuli po odbiciu od ściany \(\displaystyle{v_2=50\ \mathrm{\frac{m}{s}}}\),
- czas uderzenia ze ścianą \(\Delta t=10^{-3}\,\mathrm{s}\).

Szukane:
- zmiana pędu kuli \(\Delta p\),
- siła działająca na kulę podczas uderzenia \(F\).

Animacja

Pod obrazem animacji znajduje się przycisk. Kliknij symbol białego trójkąta w niebieskim kole, a zobaczysz symulacje zderzenia kuli ze ścianą.

Analiza sytuacji

Kula trafia prostopadle w ścianę i odbija się od niej na skutek oddziaływania ze ścianą, czyli ściana musi działać na kulę siłą, która spowoduje zmianę prędkości (i pędu) kuli. Ponieważ odbicie następuje wzdłuż linii prostopadłej do powierzchni ściany, wnioskujemy, że siła działa również wzdłuż tej prostej – w kierunku od ściany. Zakładamy, że w trakcie zderzenia, na kulę działa ze strony ściany stała siła.

Opis matematyczny

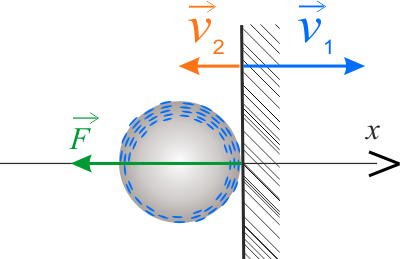
Rysunek

Załóżmy, że przed zderzeniem ze ścianą kula porusza się w prawo. Ponieważ zderzenie kuli ze ścianą zachodzi wzdłuż linii prostopadłej do powierzchni ściany, dlatego jego opis przeprowadzimy wzdłuż osi \(x\) jednowymiarowego układu współrzędnych, skierowanej prostopadle do ściany. W przedstawionym układzie współrzędnych, składowa siły działającej na kulę w czasie zderzenia ze ścianą, wynosi \(F<0\) . Zgodnie z II zasadą dynamiki, siła ta jest równa szybkości zmiany pędu:
\[\displaystyle{F=\frac{\Delta p}{\Delta t}}\]
Zmianę wartości pędu kuli, w wyniku zderzenia ze ścianą, można opisać wzorem \(\Delta p=m\,\Delta v\). Po uwzględnieniu kierunków prędkości w stosunku do obranej osi współrzędnych mamy:
\(\Delta p=m \,\left ((-v_2)-v_1  \right )=m\,(-v_2-v_1)\)
\(\Delta p=-m\,(v_2+v_1)\)

Rozwiązanie

Wyznaczmy najpierw zmianę pędu kuli w wyniku zderzenia ze ścianą.

\(\Delta p=-m\,(v_2+v_1)\)
\(\displaystyle{\Delta p=-1\cdot (100+50)=-150\,\mathrm{kg\cdot \frac{m}{s}}}\)

Siła działająca na kulę podczas uderzenia o ścianę wynosi:
\(\displaystyle{F=\frac{\Delta p}{\Delta t}=\frac{-150}{10^{-3}}=-1,5\cdot 10^5}\)  \(\displaystyle{\left [\mathrm{\frac{kg\cdot\frac{m}{s}}{s}=N} \right ]}\)

Odpowiedź

Zmiana pędu kuli wynosi \(\displaystyle{\Delta p=-1\cdot (100+50)=-150\,\mathrm{kg\cdot \frac{m}{s}}}\), natomiast wartość średniej siły działającej na kulę wynosi \(F=-1,5\cdot 10^5\,\mathrm{N}\).