Zadanie 3.2.1.6
Wskazówka: możesz wyznaczyć najpierw wartości przyspieszeń: stycznego i dośrodkowego. Czy można wyznaczyć zależność od czasu promienia krzywizny toru rzutu?
Wskazówka teoretyczna
- wektor przyspieszenia całkowitego: \(\vec{a}=\left [ a_n\,,\,a_s \right ]\),
- składowa normalna przyspieszenia \(\displaystyle{a_n=\frac{v^2}{R}}\),
- składowa styczna przyspieszenia \(\displaystyle{a_s=\frac{\mathrm{d}v }{\mathrm{d} t}}\).
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- masa wyrzuconego ciała \(m=1\,\mathrm{kg}\),
- prędkość początkowa ciała \(\displaystyle{v_0=10\,\mathrm{\frac{m}{s}}}\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}}}\).
Szukane:
- zależność od czasu wartości siły stycznej działającej na ciało \(F_s(t)\),
- zależność od czasu wartości siły dośrodkowej działającej na ciało \(F_d(t)\),
- zależność od czasu promienia krzywizny toru rzutu \(R(t)\),
- wartość siły całkowitej działającej na ciało \(F\).
Analiza sytuacji
Rzut poziomy możemy traktować jako złożenie spadku swobodnego z ruchem ze stałą prędkością, równą prędkości, z jaką rzucono ciało, w kierunku poziomym. W rzucie tym, na poruszające się ciało, działa wyłącznie siła grawitacji skierowana pionowo. Składowa siły grawitacji styczna do toru powoduje zwiększenie prędkości ciała, a składowa prostopadła jego zakrzywienie. Tak więc rozwiązanie zadania polega na rozłożeniu siły grawitacji na składową styczną i normalną (prostopadłą do stycznej) do toru.
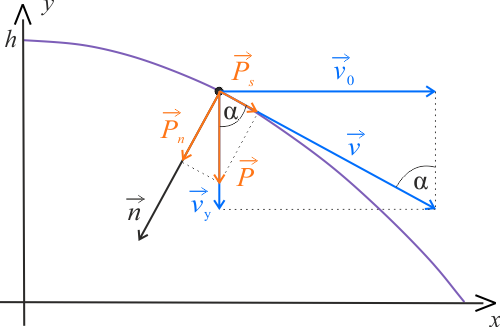
Na rysunku powyżej naszkicowano tor ciała w rzucie poziomym z zaznaczeniem siły grawitacji \(P\) i jej składowych. Jak wynika z rysunku, wartość składowej stycznej siły grawitacji jest równa:
gdzie \(\alpha\) jest kątem zawartym pomiędzy styczną do toru a kierunkiem siły grawitacji (pionem). Wartość tego kąta będzie się zmieniała wraz z czasem ruchu.
Z kinematycznego opisu rzutu poziomego z prędkością początkową \(v_0\) wiemy, że wartość prędkości wynosi:
Wartość kąta pomiędzy pionem a styczną do toru, można wyznaczyć z analizy prędkości w rzucie poziomym. Na rysunku przedstawiono wektor prędkości w danym punkcie toru, jako złożenie prędkości poziomej z prędkością pionową (prędkością spadku swobodnego \(v_y=gt\)). Wynika z niego, że:
Po podstawieniu wartości \(v\) mamy:
Wstawiając te wartości do wzorów na siły otrzymujemy:
W małym otoczeniu dowolnego punktu można zawsze, rzeczywisty fragment toru, przybliżyć fragmentem okręgu o pewnym promieniu \(R\). Promień tego okręgu nazywamy promieniem krzywizny, jego wartość będzie ulegała zmianie w czasie ruchu ciała. Zakładając, że dokonaliśmy takiego przybliżenia możemy teraz uważać siłę \(P_n\) za siłę dośrodkową w ruchu po okręgu. Zatem
Rozwiązanie
Do otrzymanych zależności można teraz podstawić wielkości liczbowe.
1. Zależność od czasu wartości siły stycznej działającej na ciało:
\[\eqalign{F_s(t) &=1\cdot 10\cdot \frac{10\,t}{\sqrt{10^2+(10\,t)^2}} \\ F_s(t) &=1\cdot 10\cdot \frac{10\,t}{10 \sqrt{1+t^2}}}\]
2. Zależność od czasu wartości siły dośrodkowej działającej na ciało:
\[\eqalign{F_d(t) &=1\cdot 10\cdot \frac{10}{\sqrt{10^2+(10\,t)^2}} \\ F_d(t) &= 10\cdot \frac{10}{10\,\sqrt{1+t^2}}}\]
\[\eqalign{\mathrm{kg\cdot \frac{m}{s^2}\cdot \frac{\frac{m}{s}}{\sqrt{\frac{m^2}{s^2}+\left ( \frac{m}{s^2}\right )^2\cdot s^2}}= \\ =N\cdot \frac{\frac{m}{s}}{\sqrt{\frac{m^2}{s^2}+\frac{m^2}{s^2}}}= \\ =N\cdot \frac{m}{s}\cdot \frac{s}{m}=N}}\]
3. Zależność od czasu promienia krzywizny toru rzutu:
\[\eqalign{\mathrm{\frac{\left ( \large{\frac{m^2}{s^2}}+\frac{m^2}{s^4}\cdot s^2 \right )\sqrt{\frac{m^2}{s^2}+\frac{m^2}{s^4}\cdot s^2}}{\large{\frac{m}{s^2}}\cdot \frac{m}{s}}= \\ =\frac{\large{\frac{m^2}{s^2}}\sqrt{\large{\frac{m^2}{s^2}}}}{\frac{m^2}{s^3}}= \\ =\frac{m^2}{s^2}\cdot \frac{m}{s}\cdot \frac{s^3}{m^2}=m}}\]
4. Zależność od czasu wartości siły całkowitej działającej na ciało:
Odpowiedź
Zależność od czasu wartości siły stycznej działającej na ciało wynosi \(\displaystyle{F_s(t)=\frac{10\,t}{\sqrt{1+t^2}}\,\mathrm{[N]} }\).
Zależność od czasu wartości siły dośrodkowej działającej na ciało wynosi \(\displaystyle{F_d(t)=\frac{10}{\sqrt{1+t^2}}\,\mathrm{[N]} }\).
Zależność od czasu promienia krzywizny toru rzutu wynosi \(\displaystyle{R(t)=10\,\left ( 1+t^2 \right )^{\frac{3}{2}}\,\mathrm{[m]} }\).
Wartość siły całkowitej działającej na ciało wynosi \(F=10\,\mathrm{N}\).
Zadanie 3.2.1.6
Wskazówka: możesz wyznaczyć najpierw wartości przyspieszeń: stycznego i dośrodkowego. Czy można wyznaczyć zależność od czasu promienia krzywizny toru rzutu?
Wskazówka teoretyczna
- wektor przyspieszenia całkowitego: \(\vec{a}=\left [ a_n\,,\,a_s \right ]\),
- składowa normalna przyspieszenia \(\displaystyle{a_n=\frac{v^2}{R}}\),
- składowa styczna przyspieszenia \(\displaystyle{a_s=\frac{\mathrm{d}v }{\mathrm{d} t}}\).
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- masa wyrzuconego ciała \(m=1\,\mathrm{kg}\),
- prędkość początkowa ciała \(\displaystyle{v_0=10\,\mathrm{\frac{m}{s}}}\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}}}\).
Szukane:
- zależność od czasu wartości siły stycznej działającej na ciało \(F_s(t)\),
- zależność od czasu wartości siły dośrodkowej działającej na ciało \(F_d(t)\),
- zależność od czasu promienia krzywizny toru rzutu \(R(t)\),
- wartość siły całkowitej działającej na ciało \(F\).
Analiza sytuacji
Na ciało o masie \(m\), poruszające się swobodnie w pobliżu powierzchni Ziemi, działa siła ciężkości o wartości \(mg\) pionowo w dół. Siłę tę można rozłożyć na składowe: styczną do toru \(F_s\) (mającą kierunek prędkości) oraz prostopadłą do toru. Tę ostatnią nazywamy albo normalną \((F_n)\), albo, tak jak w ruchu po okręgu – siłą dośrodkową \(F_d\). Nazwa, w tym przypadku, związana jest z wyobrażeniem ruchu po dowolnej krzywej, jako „kawałkami” po okręgu o zmieniającym się promieniu (promieniu krzywizny). Siły te związane są poprzez II zasadę dynamiki z odpowiednimi składowymi przyspieszeń – stycznym \(a_s\) i dośrodkowym \(a_d\).
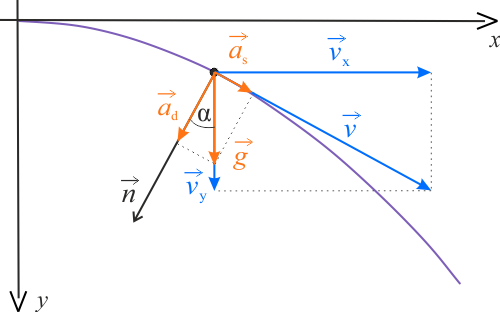
Na powyższym rysunku w układzie współrzędnych \(x\,y\), przy czym oś \(y\) jest skierowana pionowo w dół, przedstawiono, dla pewnej chwili czasu \(t\), prędkość i jej składowe \(v_x\) i \(v_y\) oraz przyspieszenie grawitacyjne \(g\), jego składową styczną \(a_s\) i dośrodkową \(a_d\). Występujące na wykresie wektory przyspieszeń są reprezentowane przez ich wartości bezwzględne, natomiast prędkość przez składowe prędkości. Składowe przyspieszenia wyrażają się wzorami:
natomiast szukane składowe siły ciężkości:
Z powyższych wzorów widać, że, aby wyznaczyć w zadaniu szukane wielkości, musimy najpierw znaleźć zależność wartości prędkości ciała od czasu. Z kinematycznego opisu rzutu poziomego z prędkością początkową \(v_0\) wiemy, że:
a stąd wartość prędkości wynosi:
W celu obliczenia wartość składowej stycznej siły, skorzystamy z przedstawionych powyżej wzorów, otrzymując:
Wartość siły dośrodkowej dana jest z kolei wzorem:
Niestety, na tym etapie, nie możemy wyznaczyć zależności od czasu wartości siły dośrodkowej, działającej na ciało, gdyż, co prawda mamy wyznaczoną zależność \(v(t)\), ale również promień krzywizny jest funkcją czasu \(R=R(t)\). Dlatego wyznaczymy najpierw dośrodkową składową \(a_d\) przyspieszenia ziemskiego. Długość wektora przyspieszenia ziemskiego można obliczyć z następującej zależności \(g^2=a_d^2+a_s^2\). Po prostych przekształceniach otrzymujemy:
Mając wyznaczoną siłę \(F_d(t)\), możemy wyznaczyć zależność od czasu promienia krzywizny toru rzutu z zależności:
Rozwiązanie
Do otrzymanych zależności można teraz podstawić wielkości liczbowe.
1. Zależność od czasu wartości siły stycznej działającej na ciało:
\[\eqalign{F_s(t) &=1\cdot 10\cdot \frac{10\,t}{\sqrt{10^2+(10\,t)^2}} \\ F_s(t) &=1\cdot 10\cdot \frac{10\,t}{10 \sqrt{1+t^2}}}\]
2. Zależność od czasu wartości siły dośrodkowej działającej na ciało:
\[\eqalign{F_d(t) &=1\cdot 10\cdot \frac{10}{\sqrt{10^2+(10\,t)^2}} \\ F_d(t) &= 10\cdot \frac{10}{10\,\sqrt{1+t^2}}}\]
\[\eqalign{\mathrm{kg\cdot \frac{m}{s^2}\cdot \frac{\frac{m}{s}}{\sqrt{\frac{m^2}{s^2}+\left ( \frac{m}{s^2}\right )^2\cdot s^2}}= \\ =N\cdot \frac{\frac{m}{s}}{\sqrt{\frac{m^2}{s^2}+\frac{m^2}{s^2}}}= \\ =N\cdot \frac{m}{s}\cdot \frac{s}{m}=N}}\]
3. Zależność od czasu promienia krzywizny toru rzutu:
\[\eqalign{\mathrm{\frac{\left ( \large{\frac{m^2}{s^2}}+\frac{m^2}{s^4}\cdot s^2 \right )\sqrt{\frac{m^2}{s^2}+\frac{m^2}{s^4}\cdot s^2}}{\large{\frac{m}{s^2}}\cdot \frac{m}{s}}= \\ =\frac{\large{\frac{m^2}{s^2}}\sqrt{\large{\frac{m^2}{s^2}}}}{\frac{m^2}{s^3}}= \\ =\frac{m^2}{s^2}\cdot \frac{m}{s}\cdot \frac{s^3}{m^2}=m}}\]
4. Zależność od czasu wartości siły całkowitej działającej na ciało:
Odpowiedź
Zależność od czasu wartości siły stycznej działającej na ciało wynosi \(\displaystyle{F_s(t)=\frac{10\,t}{\sqrt{1+t^2}}\,\mathrm{[N]} }\).
Zależność od czasu wartości siły dośrodkowej działającej na ciało wynosi \(\displaystyle{F_d(t)=\frac{10}{\sqrt{1+t^2}}\,\mathrm{[N]} }\).
Zależność od czasu promienia krzywizny toru rzutu wynosi \(\displaystyle{R(t)=10\,\left ( 1+t^2 \right )^{\frac{3}{2}}\,\mathrm{[m]} }\).
Wartość siły całkowitej działającej na ciało wynosi \(F=10\,\mathrm{N}\).
