Zadanie 3.3.1.5
Zmienna siła
Na ciało o masie \(m\) działa siła hamująca, proporcjonalna do prędkości \(F=-b\,v\,\mathrm{[N]}\), gdzie \(b\) - stała. Znajdź zależność prędkości ciała od czasu. Wyznacz równanie opisujące drogę w funkcji czasu.
Wskazówka teoretyczna
Teoria
Wybrane zależności z kinematyki
Wybrane zależności z dynamiki
- Przemieszczenie ciała
\(\displaystyle{v(t)=\frac{\mathrm{d} S}{\mathrm{d} t}}\)
- Droga przebyta przez ciała od punktu \(A\) do punktu \(B\)
\(\displaystyle{S=\int_{A}^{B}\mathrm{d} S=\int_{t_A}^{t_B}v \,\mathrm{d} t}\)
- Przyspieszenie ciała
\(\displaystyle{a=\frac{\mathrm{d} v}{\mathrm{d} t}=\frac{\mathrm{d^2} S}{\mathrm{d} t^2}}\)
Wybrane zależności z dynamiki
- II zasada dynamiki: Jeśli siły działające na ciało nie równoważą się, to ciało porusza się z przyspieszeniem wprost proporcjonalnym do siły wypadkowej, a odwrotnie proporcjonalnym do masy ciała.
\(F=am\)
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- masa ciała \(m\),
- równanie opisujące siłę hamującą \(F=-b\,v\,\mathrm{[N]}\).
Uwaga: jednostka parametru \(b\) to \(\displaystyle{\mathrm{\frac{kg}{s}}}\)
\(\displaystyle{\mathrm{N=kg\cdot \frac{m}{s^2}=\frac{kg}{s}\cdot\frac{m}{s} } }\)
Szukane:
- zależność prędkości ciała od czasu,
- równanie opisujące drogę w funkcji czasu.
Analiza sytuacji
Na ciało działa zmienna siła o wartości \(F=-b\,v\), która hamuje poruszające się ciało.
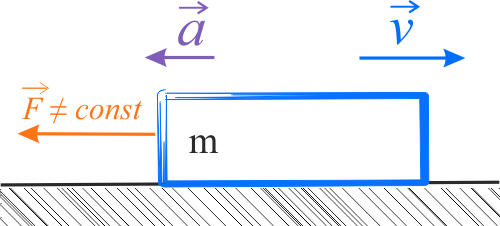
Na ciało działa siła przeciwnie skierowana do kierunku ruchu. Ciało porusza się ruchem opóźnionym ze zmiennym przyspieszeniem. Siła działająca na ciało zależy od jego prędkości, więc z czasem maleje. Do zaistniałej sytuacji można zastosować II zasadę dynamiki \(F=am\). Znalezienie zależności prędkości ciała od czasu wymaga przekształceń równania \(m\,a=-b\,v\).
Rozwiązanie
Równanie ruchu dla przypadku danego w tym zadaniu ma postać
\(m\,a=-b\,v\)
Wykorzystując definicję przyspieszenia mamy
\(\displaystyle{m\frac{\mathrm{d} v}{\mathrm{d} t}=-b\,v}\)
Otrzymane równanie różniczkowe mnożymy obustronnie przez \(\displaystyle{\frac{\mathrm{d} t}{m\,v}}\)
\(\displaystyle{\frac{\mathrm{d} v}{v}=-\frac{b}{m} \mathrm{d} t }\)
Całkujemy obustronnie
\(\displaystyle{\int \frac{\mathrm{d} v}{v}=-\frac{b}{m}\int \mathrm{d} t }\)
\[\int \frac{1}{x}\mathrm{d} x=\ln x+C\] \[\int \mathrm{d} x=x+C\]
\(\displaystyle{\ln v=-\frac{b}{m}t+C }\)
Po uwzględnieniu warunków początkowych mamy
W celu wyznaczenia stałej całkowania \(C\), podstawiamy do otrzymanego równania warunki początkowe, czyli, w chwili początkowej \(t=0\), prędkość wynosi \(v=v_0\). \[\displaystyle{\ln v_0=-\frac{b}{m}\cdot 0+C }\] \[\ln v_0=C\] Otrzymaną wartość stałej podstawiamy do równania i otrzymujemy:
\(\displaystyle{\ln v=-\frac{b}{m}t+\ln v_0 }\)
\(\displaystyle{\ln v-\ln v_0=-\frac{b}{m}t }\)
\(\displaystyle{\ln \frac{v}{v_0}=-\frac{b}{m}t }\)
Otrzymane równanie można przekształcić do postaci
\[e^{\Large{\ln \frac{v}{v_0}}}=e^{\Large{-\frac{b}{m}t}} \] \[\displaystyle{\frac{v}{v_0}=e^{-\Large{\frac{b}{m}t}}}\]
\(v=v_0 e^{-\Large{\frac{b}{m}t}} \)
Zależność prędkości ciała od czasu ma postać:
\(v(t)=v_0 e^{-\Large{\frac{b}{m}t}} \)
Wyprowadzenie zależności drogi od czasu wymaga użycia definicji \(\displaystyle{v(t)=\frac{\mathrm{d} S}{\mathrm{d} t}}\):
\(\displaystyle{\frac{\mathrm{d} S}{\mathrm{d} t}=v_0 e^{-\Large{\frac{b}{m}t}} }\)
Mnożymy obie strony przez \(\mathrm{d} t\) i całkujemy:
\(\displaystyle{\int \mathrm{d} S=v_0 \int e^{-\Large{\frac{b}{m}t}}\mathrm{d} t }\)
\[\int e^x \mathrm{d}x=e^x+C\] \[\int e^{\Large{\frac{a}{b}x}}\mathrm{d}x=\frac{b}{a}e^{\Large{\frac{a}{b}x}}+C\]
\(\displaystyle{S=-\frac{v_0m}{b}e^{-\Large{\frac{b}{m}t}}+C }\)
Po uwzględnieniu warunków początkowych mamy
W celu wyznaczenia stałej całkowania \(C\), podstawiamy do otrzymanego równania warunki początkowe, czyli, w chwili początkowej \(t=0\) oraz \(S=0\). \[\displaystyle{0=-\frac{v_0m}{b}e^{-\Large{\frac{b}{m}\cdot 0}}+C }\] \[\displaystyle{\frac{v_0m}{b}e^0=C}\] \[\displaystyle{C=\frac{v_0m}{b}}\] Otrzymaną wartość stałej podstawiamy do równania i otrzymujemy:
\(\displaystyle{S=\frac{v_0m}{b}\left (1-e^{-\Large{\frac{b}{m}t}}\right ) }\)
Zależność drogi od czasu ma postać:
\(\displaystyle{S(t)=\frac{v_0m}{b}\left (1-e^{-\Large{\frac{b}{m}t}}\right ) }\)
Ciało zatrzyma się, gdy jego prędkość zmaleje do zera. Nastąpi to w nieskończenie długim czasie, ponieważ
Droga jaką przebędzie ciało do chwili zatrzymania się wynosi \(\displaystyle{S_k=\frac{v_0m}{b}}\), gdyż
\(\lim_{t\rightarrow \infty }\,v_0 e^{-\Large{\frac{b}{m}t}}=0\)
Droga jaką przebędzie ciało do chwili zatrzymania się wynosi \(\displaystyle{S_k=\frac{v_0m}{b}}\), gdyż
\(\displaystyle{\lim_{t\rightarrow \infty }\,\frac{v_0m}{b}\left (1-e^{-\Large{\frac{b}{m}t}}\right )=\frac{v_0m}{b} }\)
Odpowiedź
Zależność prędkości ciała od czasu ma postać \(v(t)=v_0 e^{-\Large{\frac{b}{m}t}} \), natomiast równanie opisujące drogę w funkcji czasu wygląda następująco \(\displaystyle{S(t)=\frac{v_0m}{b}\left (1-e^{-\Large{\frac{b}{m}t}}\right ) }\).