Zadanie 3.3.1.4
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.3. Tarcie, opory i zmienna siła
  4. 3.3.1 Nauka
  5. Zadanie 3.3.1.4

 Zadanie 3.3.1.4

Siła tarcia kinetycznego
Na lodzie poukładane są na sobie trzy paczki (rysunek poniżej). Do paczki pierwszej, leżącej na wierzchu, przymocowano sznurek i pociągnięto z siłą \(F=200\,\mathrm{N}\). Oblicz przyspieszenia, z jakimi poruszają się paczki. Określ kierunek ich ruchu. Masy paczek wynoszą: \(m_1=20\,\mathrm{kg}\), \(m_2=20\,\mathrm{kg}\) oraz \(m_3=200\,\mathrm{kg}\). Współczynnik tarcia kinetycznego między paczką pierwsza a drugą wynosi \(\mu_{12}=0,2\), natomiast pomiędzy paczką drugą a trzecią \(\mu_{23}=0,3\).

 Wskazówka teoretyczna

 Teoria - tarcie kinetyczne
Tarcie kinetyczne (dynamiczne) - występuje, gdy dwie powierzchnie poruszają się względem siebie, ma stałą wartość. Jest to siła styczna do powierzchni dwóch ciał.
Siła tarcia kinetycznego jest to siła styczna do powierzchni dwóch ciał przemieszczających się względem siebie. 

\(T_k=\mu_k N\),

gdzie \(\mu_k\) jest współczynnikiem tarcia kinetycznego, a \(N\) siłą reakcji podłoża.
Rysunek

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa paczki pierwszej \(m_1=20\,\mathrm{kg}\),
- masa paczki drugiej \(m_2=20\,\mathrm{kg}\),
- masa paczki trzeciej \(m_3=200\,\mathrm{kg}\),
- siła, z jaką ciągnięta jest paczka pierwsza \(F=200\,\mathrm{N}\),
- współczynnik tarcia kinetycznego między paczką pierwsza a drugą \(\mu_{12}=0,2\),
- współczynnik tarcia kinetycznego między paczką drugą a trzecią \(\mu_{23}=0,3\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}}}\).

Szukane:
- przyspieszenie paczki pierwszej \(a_1\),
- przyspieszenie paczki drugiej \(a_2\),
- przyspieszenie paczki trzeciej \(a_3\),
- kierunki przyspieszeń.

Analiza sytuacji

Przeanalizujmy po kolei siły działające na paczki. Zacznijmy od paczki pierwszej.

1. Siły działające na paczkę pierwszą.

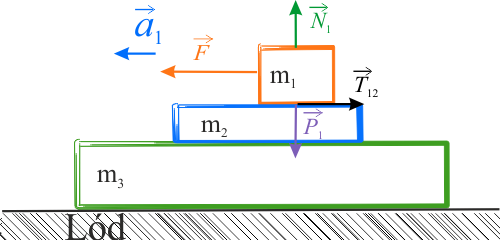
Rysunek 1


 Na paczkę pierwszą działa siła \(\vec{F}\), powodująca ruch jednostajnie przyspieszony w lewo. W kierunku poziomym, działa jeszcze siła tarcia kinetycznego \(\vec{T}_{12}\), skierowana przeciwnie do sił \(\vec{F}\).  
\(\sum F_x=F-T_{12}=m_1\,a_1\)
Po rozpisaniu siły tarcia kinetycznego mamy:
\(a_1\,m_1=F-\mu_{12}\,m_1\,g\)
 W kierunku pionowym działają dwie siły, które wzajemnie się równoważą, nie powodując ruchu. Jest to ciężar paczki \(P_1=m_1\,g\) oraz siła reakcji podłoża \(N_1\). Siły te mają taka sama wartość, ale przeciwne zwroty.  
\(\sum F_y=N_1-P_1=0\)


2. Siły działające na paczkę drugą.
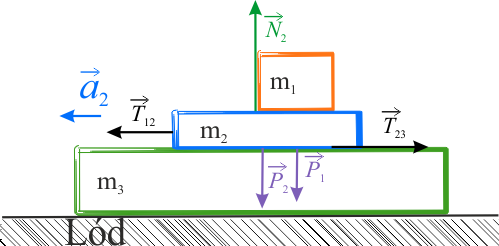
Rysunek 2


 Na ciało pierwsze działa siła tarcia. Zgodnie z III zasadą dynamiki Newtona, siła tarcia występująca pomiędzy tymi ciałami, działa również na ciało drugie. Wartość tej siły \(T_{12}\) jest ta sama a zwrot przeciwny. Omawiana siła wpływa na ruch paczki drugiej. Na tym etapie zakładamy, że paczka druga porusza się w lewo. Kierunek ruchu tej paczki zależy od tego, która siła tarcia jest większa \(T_{12}\) czy \(T_{23}\). Siła \(T_{23}\) ma inną wartość oraz przeciwny zwrot w stosunku do siła \(T_{12}\). 
\(\sum F_x=T_{12}-T_{23}=m_2\,a_2\)
Po rozpisaniu sił tarcia kinetycznego mamy:
\(a_2\,m_2=\mu_{12\,}m_1\,g-\mu_{23}\,g(m_1+m_2)\)
 W kierunku pionowym działają trzy siły, które wzajemnie się równoważą, nie powodując ruchu. Jest to ciężar paczki pierwszej \(P_1=m_1\,g\) oraz drugiej \(P_2=m_2\,g\) - siły działające w tym samym kierunku. Siła reakcji podłoża \(N_2\) jest równoważna, co do wartości, ciężarom \(P_1+P_2\). 
\(\sum F_y=N_2-P_1-P_2=0\)

3. Siły działające na paczkę trzecią.
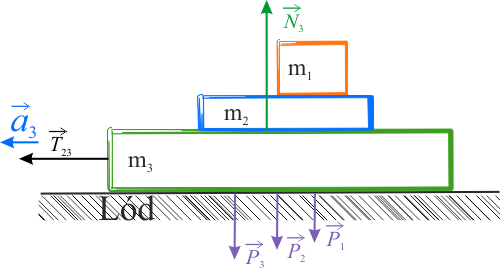
Rysunek 3


 Siła tarcia działająca pomiędzy ciałami \(m_2\) oraz \(m_3\), zgodnie z III zasadą dynamiki Newtona, działa na paczkę trzecią. Siła ta wpływa na ruch ostatniej paczki i będzie skierowany w lewo. Paczka ślizga się po lodzie, co oznacza brak tarcia miedzy trzecią paczką a podłożem. 
\(\sum F_x=T_{23}=m_3\,a_3\)
Po rozpisaniu siły tarcia kinetycznego otrzymujemy:
\(a_3\,m_3=\mu_{23}\,g(m_1+m_2)\)
 W kierunku pionowym działają cztery siły, które wzajemnie się równoważą, nie powodując ruchu. Jest to ciężar paczki pierwszej \(P_1=m_1\,g\), drugiej \(P_2=m_2\,g\) oraz trzeciej \(P_3=m_3\,g\) - siły działające w tym samym kierunku. Siła reakcji podłoża \(N_3\) jest równoważna, co do wartości, ciężarom \(P_1+P_2+P_3\). 
\(\sum F_y=N_3-P_1-P_2-P_3=0\)

Podsumowanie.

W efekcie powyższych rozważań otrzymaliśmy układ trzech równań:
\[\left\{\begin{matrix}a_1\,m_1= &F-\mu_{12}\,m_1\,g \\ a_2\,m_2= &\mu_{12}\,m_1\,g-\mu_{23}\,g(m_1+m_2)\\ a_3\,m_3= &\mu_{23}\,g(m_1+m_2) \end{matrix}\right.\]

Rozwiązanie

Odpowiedź na pytanie, sformułowane w zadaniu, otrzymamy po rozwiązaniu układu równań:
\[\left\{\begin{matrix}a_1\,m_1= &F-\mu_{12}\,m_1\,g \\ a_2\,m_2= &\mu_{12}\,m_1\,g-\mu_{23}\,g(m_1+m_2)\\ a_3\,m_3= &\mu_{23}\,g(m_1+m_2) \end{matrix}\right.\]
Z pierwszego równania mamy:

\(\displaystyle{a_1=\frac{F}{m_1}-\mu_{12}\,g}\).
Po podstawieniu wartości liczbowych, otrzymujemy:
\(\displaystyle{a_1=\frac{200}{20}-0,2\cdot 10=8\,\mathrm{\frac{m}{s^2}}}\).

Z drugiego równania, po  \[\displaystyle{a_2=\frac{\mu_{12}m_1\,g-\mu_{23}\,g(m_1+m_2)}{m_2}}\] \[\displaystyle{a_2=\frac{\mu_{12}m_1\,g-\mu_{23}\,gm_1-\mu_{23}\,gm_2}{m_2} }\]  , otrzymujemy:
\(\displaystyle{a_2=\frac{g\,m_1(\mu_{12}-\mu_{23})}{m_2}-\mu_{23}\,g }\).
Po podstawieniu wartości liczbowych, mamy:
\(\displaystyle{a_2=\frac{10\cdot 20\cdot (0,2-0,3)}{20}-0,3\cdot 10 =-4\,\mathrm{\frac{m}{s^2}}}\).
Wartość przyspieszenie \(a_2\) jest ujemna, co oznacza, że niepoprawnie został obrany kierunek ruchu paczki drugiej. Paczka ta będzie poruszać się w prawo.

Z trzeciego równania otrzymujemy:
\(\displaystyle{a_3=\frac{\mu_{23}\,g\,(m_1+m_2)}{m_3} }\).

Po podstawieniu wartości liczbowych, otrzymujemy:
\(\displaystyle{a_3=\frac{0,3\cdot 10\cdot (20+20)}{200}=0,6\,\mathrm{\frac{m}{s^2}}}\).

Informacja

Poniżej znajduje się animacja, ilustrująca omawianą sytuację. Klikając w niebieskie kółka z cyframi, zobaczysz kolejne etapy analizy kierunków ruchu paczek.

Odpowiedź

Przyspieszenia paczek wynoszą: \(\displaystyle{a_1=8\,\mathrm{\frac{m}{s^2}}}\), \(\displaystyle{a_2=-4\,\mathrm{\frac{m}{s^2}}}\) oraz \(\displaystyle{a_3=0,6\,\mathrm{\frac{m}{s^2}}}\). Paczka pierwsza i trzecia poruszają się w kierunku działania siły \(\vec{F}\), natomiast paczka druga porusza się w stronę przeciwną.