Analiza sytuacji

Przystępując do analizy zadania, od razu można stwierdzić, że pod względem ilości działających sił zadanie nie należy do skomplikowanych. Na spadochroniarza działają tylko dwie siły: działająca pionowo w dół siła ciężkości \(F\) oraz działająca pionowo w górę siła oporu \(R\). Obie zostały pokazane na poniższym rysunku. Problemem jest zmienność siły oporu w zależności od prędkości spadochroniarza.

×

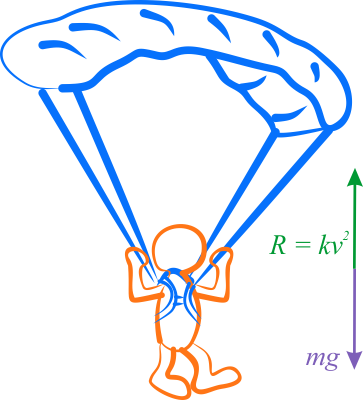
Konieczne jest rozpatrzenie układu w czasie. W momencie wyskoczenia spadochroniarza z samolotu jego prędkość pionowa wynosi zero, więc opór powietrza, zależny od tej prędkości, także wynosi zero. Wraz z upływem czasu przyciąganie ziemskie powoduje stałe zwiększenie prędkości spadania skoczka, co automatycznie przekłada się na wzrost oporu powietrza, działającego na czaszę spadochronu. Zgodnie z podanym w danych wzorem \(R=kv^2\), siła tworzona przez ten opór rośnie w funkcji kwadratowej, co oznacza jej szybki wzrost w stosunku do stałej, niezmiennej w czasie siły ciężkości \(F=mg\).

Doprowadza to do sytuacji, w której siła oporu powietrza \(R\) zrównuje się, co do wartości, z siłą ciężkości \(F\). Wtedy, zgodnie z I zasadą dynamiki Newtona, prędkość spadochroniarza ustala się na jednym poziomie i pozostaje niezmienna aż do wylądowania.

Obliczenie prędkości \(v\) wykonamy dla momentu, w którym siła ciężkości \(F\) (o stałej wartości równej \(mg\)) zrównoważy się z siłą oporu powietrza \(R\) (o wartości rosnącej wraz ze wzrostem prędkości według zależności \(kv^2\)). W momencie tym wartość prędkości ustala się i układ zachowuje się zgodnie z I zasadą dynamiki Newtona, możemy więc użyć wzoru:

\[\eqalign{ \sum{F} &= 0 \\ R-F &= 0 \\ kv^2-mg &= 0 }\]

Rozwiązanie

Przekształcając otrzymane równanie \(kv^2-mg= 0\), otrzymujemy:
\[\eqalign{ kv^2 &= mg\\ v^2 &= \frac{mg}{k} }\]
Teraz wystarczy podstawić wartości liczbowe: \[\eqalign{ v &= \sqrt{\frac{mg}{k}}= \\& = \sqrt{\frac{70\cdot10}{50}\ \mathrm{\begin{bmatrix} \frac{kg\cdot\frac{m}{s^2}}{N\frac{s^2}{m^2}}\end{bmatrix}}} =\\& = \sqrt{14\ \mathrm{\begin{bmatrix}\frac{\cancel{N}}{\cancel{N}\frac{s^2}{m^2}}\end{bmatrix}}} =\\ & = 3,74\ \mathrm{\frac{m}{s}} }\]

 Komentarz  Na spadochroniarza działa również siła wyporu powietrza w górę, ale jest ona nieporównywalnie mniejsza od sił ciężkości i oporu powietrza, wobec czego można ją pominąć w obliczeniach.