Zadanie 3.3.1.2
  1. Ewa Frączek. Kurs obliczeniowy z fizyki.
  2. 3. Zasady dynamiki
  3. 3.3. Tarcie, opory i zmienna siła
  4. 3.3.1 Nauka
  5. Zadanie 3.3.1.2
DOI: 10.37190/OZE-FizykaCw1-r3

 Zadanie 3.3.1.2

Tarcie statyczne
Turysta, którego masa wraz z plecakiem wynosi \(80\,\mathrm{kg}\), chce wejść na pagórek po oblodzonym zboczu, nachylonym do poziomu pod kątem \(15^{\circ}\). Współczynnik tarcia statycznego między podeszwami jego butów, a zboczem wynosi \(0,3\). Sprawdź, czy turysta może wejść ruchem jednostajnym na ten pagórek. Oblicz, jaki mógłby być maksymalny kąt nachylenia oblodzonego zbocza pagórka, po którym turysta mógłby wchodzić w tych butach.

 Wskazówka teoretyczna

 Teoria - tarcie statyczne i kinetyczne
Tarcie statyczne (spoczynkowe) - ma miejsce, gdy powierzchnie nie przemieszczają się względem siebie. Siła tarcia równoważy wtedy siły działające na ciało.
Maksymalna siła tarcia statycznego spełnia warunek:

\(T_s=\mu_s N\),

gdzie \(\mu_s\) jest współczynnikiem tarcia statycznego, a \(N\) siłą reakcji podłoża.

Tarcie kinetyczne (dynamiczne) - występuje, gdy dwie powierzchnie poruszają się względem siebie, ma stałą wartość. Jest to siła styczna do powierzchni dwóch ciał.
Siła tarcia kinetycznego jest to siła styczna do powierzchni dwóch ciał przemieszczających się względem siebie. 

\(T_k=\mu_k N\),

gdzie \(\mu_k\) jest współczynnikiem tarcia kinetycznego, a \(N\) siłą reakcji podłoża.

Współczynnik tarcia kinetycznego jest mniejszy od współczynnika tarcia statycznego.

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa człowieka \(m=80\,\mathrm{kg}\),
- kąt nachylenia zbocza \(\alpha=15^{\circ}\),
- współczynnik tarcia statycznego między podeszwami bu­tów człowieka a zboczem \(\mu=0,3\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}}}\).

Szukane:
- sprawdzenie, czy kąt nachylenia zbocza i współczynnik tarcia umożliwia wejście,
- maksymalny kąt nachylenia zbocza, przy którym możliwe jest wejście na zbocze \(\alpha_{max}\).

Analiza sytuacji

Na rysunku poniżej przedstawiono diagram wektorowy sił, które działają na człowieka. Na diagramie przedstawiono siły w układzie współrzędnych \(x y\), gdzie oś \(x\) i jest skierowana równolegle do zbocza w gorę, a oś \(y\) jest do niej prostopadła i skierowana w górę. Siły są reprezentowane przez ich wartości bezwzględne.

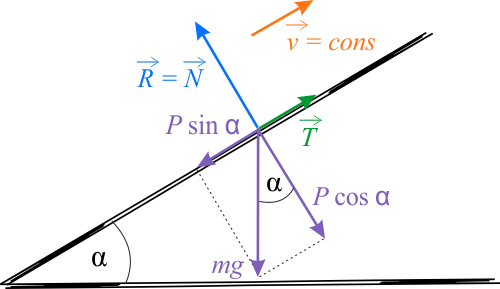
Rysunek


Na podstawie diagramu i I zasady dynamiki otrzymujemy warunek równowagi sił:
\(\eqalign{\sum F_x &=T-mg\sin \alpha=0 \\ \sum F_y &=R-mg\cos \alpha=0}\)

W zadaniu należy sprawdzić, czy siła tarcia między podeszwami butów człowieka a zboczem, nie przewyższa krytycznej wartości tarcia statycznego, jeżeli nie to trzeba znaleźć tą krytyczną wartość. W tym celu należy posłużyć się powyższymi równaniami.

Rozwiązanie

Analizując działające siły otrzymaliśmy układ równań:

\(\left\{\begin{matrix} T-mg\sin \alpha=0 \\ R-mg\cos \alpha=0 \end{matrix}\right.\)

Z pierwszego równania otrzymujemy warunek sił równoległych do zbocza

\(T=mg\sin \alpha\)
\(T=80\cdot 10\cdot \sin 15^{\circ}=207\,\mathrm{N}\)

Aby warunek z zadania był spełniony, siła tarcia statycznego nie może przewyższać swej maksymalnej wartości równej \(T_{max}=\mu N\) , gdzie \(N\) siła nacisku na powierzchnię zbocza, która, zgodnie z III zasadą dynamiki, jest równa sile \(R\), a ta z drugiego równania wynosi \(R=mg\cos \alpha\). Maksymalna wartość siły tarcia wynosi:
\(T_{max}=\mu mg \cos\, \alpha\)
\(T_{max}=0,3\cdot 10\cdot 80\cdot \cos 15^{\circ}=232\,\mathrm{N}\)

Jak widać \(T
\(mg\, \sin \alpha_{kr}= \mu mg\, \cos \alpha_{kr}\)
\(\displaystyle{\mu=\frac{\sin \alpha_{kr}}{\cos \alpha_{kr}} }\)
\(\alpha_{gr}=\operatorname{arc \operatorname{tg}{\mu}} \)
\(\alpha_{gr}=\operatorname{arc \operatorname{tg}{0,3}}=16,7^{\circ} \)

Kąt nachylenia zbocza jest prawie kątem krytycznym, więc człowiek musi uważać, aby nie przyspieszyć, co technicznie oznacza, że nie może działać podeszwami butów dodatkową siłą styczną w dół, aby przyspieszyć.

Czy turysta, wchodząc po zboczu i chcąc zwiększyć nieco szybkość, może podbiec? Jaka jest wartość tego przyspieszenia?

Maksymalne przyspieszenie człowieka, przy którym możliwe jest wejście na zbocze, to takie, że \(T=T_{max}\), czyli:

\(m(g\,\sin \alpha+a_{max})=\mu mg\,\cos\alpha\).

Stąd otrzymujemy:
\(a_{max}=g(\mu \,\cos\alpha-\sin\alpha) \)
\(\displaystyle{a_{max}=10(0,3\cdot \cos 15^{\circ} -\sin 15^{\circ})\approx 0,31\,\mathrm{\frac{m}{s^2}}} \)

Odpowiedź

Turysta może wejść ruchem jednostajnym na ten pagórek. Idąc w ten sposób wszedłby na wzgórze o kącie nachylenia stoku wynoszącym maksymalnie \(16,7^{\circ}\).