Zadanie 3.3.2.1
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- współczynnika tarcia statycznego \(\mu_s=0,3\),
- współczynnika tarcia kinetycznego \(\mu_k=0,2\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}}}\).
Szukane:
- wartość przyspieszenia skrzyni \(a\).
Odpowiedź
Skrzynia będzie poruszać się z przyspieszeniem równym \(\displaystyle{a=1\,\mathrm{\frac{m}{s^2}}}\).
Polecenie
Poniżej przedstawione są trzy stwierdzenia. Wybierz jedno prawidłowe.
Współczynnik tarcia statycznego jest większy od współczynnika tarcia kinetycznego.
W zadaniu nie ma podanej masy skrzyni, więc należy przyjąć wartość \(m=100\,\mathrm{kg}\).
Polecenie
Zastanów się nad równaniem potrzebnym do otrzymania prawidłowej odpowiedzi. Poniżej podano cztery propozycje. Wybierz jedną prawidłową.
Rozwiązanie
Poniżej pokazano rysunek z zaznaczonymi siłami działającymi na skrzynię.
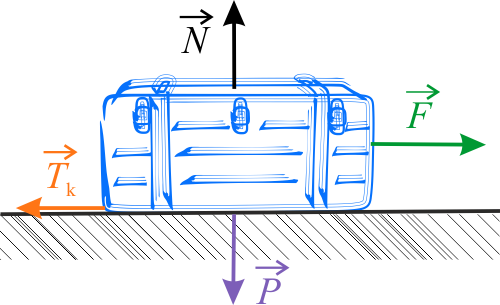
Ciężar \(\vec{P}\) oraz siła reakcji podłoża \(\vec{N}\) równoważą się, nie powodując ruchu pionowego. W płaszczyźnie poziomej, wzdłuż podłoża, działa siła \(\vec{F}\). Siła ta spowoduje ruch w momencie, gdy wartość jej będzie równa sile tarcia statycznego \(\vec{T}_s\). Działając dalej z siłą \(F=T_s\), sprawimy, że skrzynia będzie poruszać się ruchem jednostajnie przyspieszonym z przyspieszeniem \(\vec{a}\). Tarcie, jakie będzie działać na skrzynię w trakcie ruchu, jest tarciem kinetycznym. Tak, więc mamy:
Polecenie
Oblicz wartość przyspieszenie skrzyni. Wybierz jedną prawidłową wartość przyspieszenie, wśród czterech przedstawionych poniżej.
Rozwiązanie
Wynik otrzymujemy po podstawieniu wartości liczbowych do równania
Odpowiedź
Skrzynia będzie poruszać się z przyspieszeniem równym \(\displaystyle{a=1\,\mathrm{\frac{m}{s^2}}}\).
