Zadanie 3.3.2.2
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- masa cegły \(m=2\,\mathrm{kg}\),
- krytyczny kąt nachylenia deski \(\alpha_k=45^{\circ}\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}}}\).
Szukane:
- współczynnik tarcia statycznego między cegłą a deską \(\mu_s\).
Odpowiedź
Współczynnik tarcia statycznego między ciałem i deską wynosi \(\mu_s=1\).
Polecenie
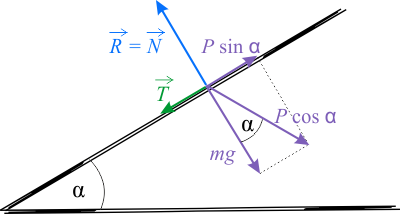
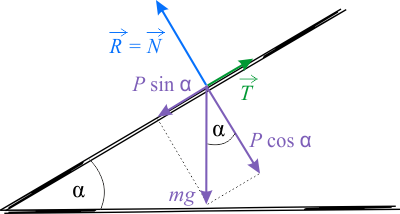
Zastanów się jakie siły działają na cegłę. Narysuj diagram sił, a następnie wybierz jeden prawidłowy rysunek wśród dwóch pokazanych poniżej.
Rozwiązanie
Na cegłę działają następujące siły: siła ciężkości \(mg\) pionowo dół, siła reakcji podłoża deski \(R\) prostopadle do powierzchni oraz siła tarcia statycznego \(T\) równolegle do powierzchni deski (siła ta zapobiega zsuwaniu się cegły w dół). Gdy cegła jest w spoczynku to, zgodnie z I zasadą dynamiki, wypadkowa sił jest równa zeru. Z treści zadania wynika, że stan równowagi zostaje zakłócony, gdy nachylenie deski osiągnęło kąt równy \(45^{\circ}\). Wnioskujemy z tego, że przy tym kącie, siła tarcia statycznego osiągnęła swoją maksymalną wartość.
Polecenie
Wyznacz współczynnik tarcia statycznego występującego pomiędzy cegłą a deską. Wybierz jedna prawidłową wartość, wśród czterech przedstawionych poniżej.
\(\mu_s=0,2\)
Rozwiązanie
Na rysunku przedstawiono diagramy sił w układzie współrzędnych \(x\,y\). Na diagramie siły reprezentowane są przez ich wartości bezwzględne. Oś \(x\) jest równoległa do powierzchni deski i skierowana w dół, a oś \(y\) jest do niej prostopadła i skierowana w górę. Na diagramie siłę ciężkości (grawitacji) rozłożono na dwie składowe: równoległą o wartości \(mg\sin \alpha\) i prostopadłą do deski, \(mg\cos \alpha\). Składowa prostopadła jest, co do wartości, równa wartości siły, jest siły \(N\) nacisku cegły na deskę. Siła ta, zgodnie z III zasadą dynamiki, jest równa, co do wartości, sile reakcji \(R\)
Oznacz to, że dla kątów \(\alpha<\alpha_k\) siła tarcia statycznego równoważy składową siły grawitacji równoległą do deski. Cegła zaczyna się zsuwać, gdy składowa siły grawitacji, skierowana równolegle do deski, przewyższy siłę tarcia statycznego. Tak, zgodnie z treścią zadania, stanie się, gdy nachylenie deski osiągnie krytyczny kąt \(\alpha_k=45^{\circ}\). Wnioskujemy, że dla tego kąta siła tarcia statycznego osiągnie swoją maksymalną wartość
\[mg\sin \alpha=mg\mu_s \cos\alpha_k\] \[\sin \alpha=\mu_s \cos\alpha_k\] \[\displaystyle{\frac{\sin\alpha_k}{\cos\alpha_k}=\mu_s}\] \[\mu_s=\operatorname{tg}{\alpha_k}\]
Odpowiedź
Współczynnik tarcia statycznego między ciałem i deską wynosi \(\mu_s=1\).