Zadanie 3.3.2.3
Informacja
Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.
Dane i szukane
Dane:
- masa balonu \(M=300\,\mathrm{kg}\),
- prędkością balonu \(\displaystyle{v=3\,\mathrm{\frac{m}{s}}}\),
- wartość siły oporu powietrza \(R=b\,v\), gdzie \(\displaystyle{b=100\,\mathrm{\frac{Ns}{m}}}\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}}}\).
Szukane:
- masa balastu należy jaką wyrzucić z balonu \(m\).
Odpowiedź
Aby balon poruszał się z prędkością \(\displaystyle{3\,\mathrm{\frac{m}{s}}}\), należy wyrzucić \(60\, \mathrm{kg}\) balastu.
Polecenie
Wybierz, wśród dwóch, jedno stwierdzenie pasujące do treści zadania.
Ponieważ balon ma poruszać się zarówno w dół i w górę ze stałą prędkością, to zgodnie z I zasadą dynamiki, wypadkowa sił jest równa zeru.
Ponieważ balon ma poruszać się zarówno w dół i w górę ze stałą prędkością, to zgodnie z II zasadą dynamiki, wypadkowa sił jest równa zeru.
Analiza sytuacji
Ponieważ balon ma poruszać się zarówno w dół i w górę ze stałą prędkością to zgodnie z I zasadą dynamiki, wypadkowa sił jest równa zeru. Druga zasada dynamiki mówi nam o efekcie działania siły na swobodne ciało. Siła nadaje ciału przyspieszenie, czyli zmienia prędkość ciała. Z treści zadania wynika, że ciało nie ma przyspieszać, tylko poruszać się ze stałą prędkością.
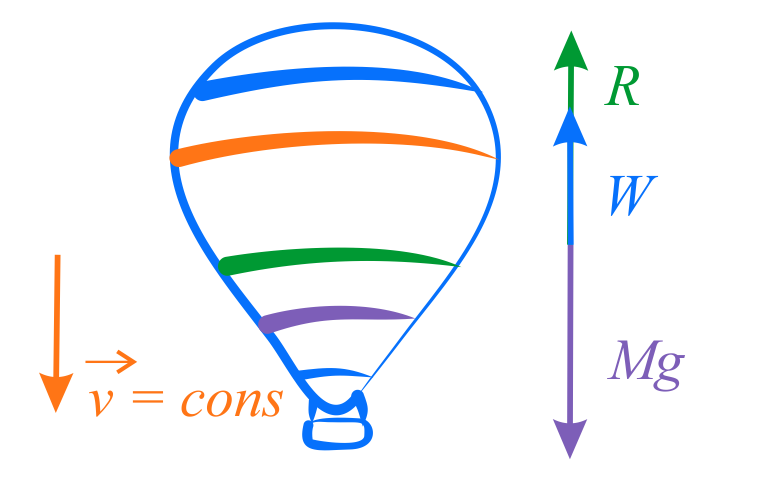
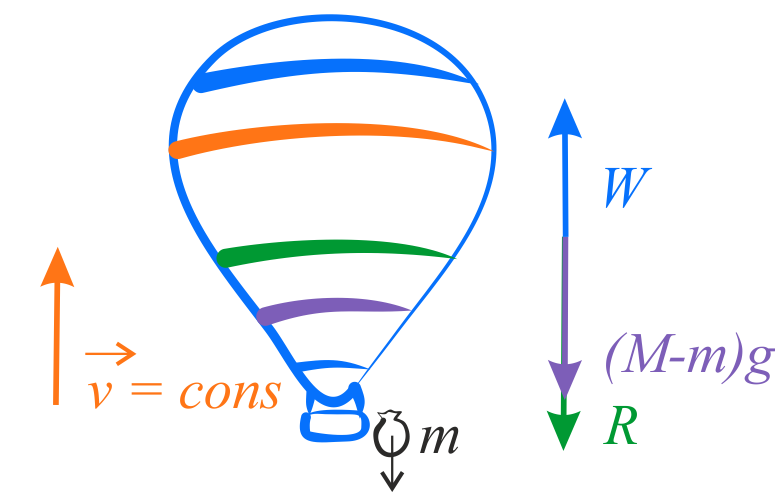
Na balon działają trzy siły: siła ciężkości, siła wyporu powietrza \(W\) oraz siła oporu \(R\). Siła ciężkości przy ruchu balonu w dół wynosi \(Mg\), a przy ruchu w górę, po wyrzuceniu balastu o masie \(m\), wynosi \((M – m)g\). Kierunek siły oporu powietrza jest przeciwny do kierunku ruchu balonu.
Na rysunkach poniżej przedstawiono diagramy sił dla obu przypadków w jedno-wymiarowym układzie współrzędnych - osi \(y\) skierowanej w górę. Na diagramach siły są reprezentowane przez ich wartości bezwzględne.
Polecenie
Oblicz masę balastu, jaką należy wyrzucić z balonu, aby wznosił się on z prędkością \(\displaystyle{3\,\mathrm{\frac{m}{s}}}\). Poniżej przedstawione są cztery wyniki. Wybierz jeden prawidłowy.
\(m=20\,\mathrm{kg}\)
Rozwiązanie
Zgodnie z I zasadą dynamiki warunki równowagi sił dla obu przypadków mają postaci:
- dla opadania balonu
- dla wznoszenia balonu
W ten sposób otrzymaliśmy układ z dwoma niewiadomymi \(m\) oraz \(R\).
Po \[\left\{\begin{matrix} W=& Mg-R\\ W=&(M-m)g+R \end{matrix}\right.\] \[Mg-R=Mg-mg+R\] \[0=-mg+R+R\] \[mg=2R\] otrzymujemy:
Zauważmy, że aby spowodować ruch ze stałą prędkością o takiej samej wartości w górę, jak prędkość opadania, należy wyrzucić masę balastu, która nie zależy od masy samego balonu.
Odpowiedź
Aby balon poruszał się z prędkością \(\displaystyle{3\,\mathrm{\frac{m}{s}}}\), należy wyrzucić \(60\, \mathrm{kg}\) balastu.