Zadanie 3.3.2.4
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.3. Tarcie, opory i zmienna siła
  4. 3.3.2 Trening
  5. Zadanie 3.3.2.4

 Zadanie 3.3.2.4

Siła tarcia kinetycznego
Na platformie na kółkach o masie \(100\,\mathrm{kg}\) położono skrzynię o masie \(20\,\mathrm{kg}\). Do skrzyni zamontowano sznur i zaczęto za niego ciągnąć ze stała siłą \(200\,\mathrm{N}\). Ile wynosi przyspieszenie platformy i skrzyni, jeżeli wiadomo, że współczynnik tarcia kinetycznego między skrzynią a platformą wynosi \(0,2\).

Informacja

Możesz zobaczyć odpowiedź klikając w przycisk "Odpowiedź" lub sprawdzać kolejne etapy rozwiązania, wybierając prawidłowe odpowiedzi. W rozwiązaniu znajdziesz wskazówki, obliczenia i objaśnienia.

Dane i szukane

Dane:
- masa skrzyni \(m_1=20\,\mathrm{kg}\),
- masa platformy \(m_2=100\,\mathrm{kg}\),
- siła działająca na skrzynię \(F=200\,\mathrm{N}\),
- współczynnik tarcia kinetycznego między skrzynią a platformą \(\mu_k=0,2\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}}}\).

Szukane:
- przyspieszenie skrzyni \(a_1\),
- przyspieszenie platformy \(a_2\).

Odpowiedź

Przyspieszenie skrzyni wynosi \(\displaystyle{a_1=8\,\mathrm{\frac{m}{s^2}}}\), natomiast platformy ma wartość \(\displaystyle{a_2=0,4\,\mathrm{\frac{m}{s^2}}}\).

Polecenie

Rozrysuj siły działające na skrzynię i platformę, a następnie napisz równania opisujące tę sytuację. Wybierz jeden prawidłowy układ równań, spośród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\left\{\begin{matrix} 0=& F-T_k\\ 0=&T_k-mg \end{matrix}\right.\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(\left\{\begin{matrix} a_1m_1=& F-T_k\\ a_2m_2=&T_k \end{matrix}\right.\)

Odpowiedź prawidłowa

Wybór 3 z 4

\(\left\{\begin{matrix} a_1m_1=& T_k\\ a_2m_2=&F-T_k \end{matrix}\right.\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(\left\{\begin{matrix} 0=& N-mg-F-T_k\\ 0=&mg-N+T_k \end{matrix}\right.\)

Odpowiedź nieprawidłowa

Rozwiązanie

Na poniższym rysunku pokazano siły działające na układ ciał w płaszczyźnie poziomej. Siły działające w płaszczyźnie pionowej są w równowadze i nie powodują ruchu.

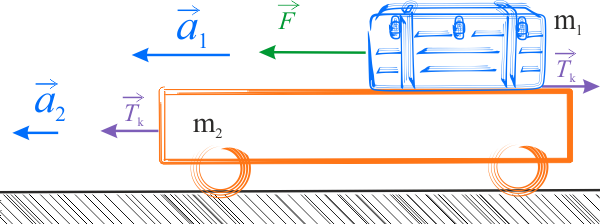
Rysunek


Pierwsze równanie dotyczy sił działających na skrzynię. Na rysunku widać, że ruch skrzyni powoduje siała \(F\). Sile tej przeciwstawia się siła tarcia kinetycznego \(T_k\), więc siła wypadkowa wynosi \(F-T_k\). Pierwsze równanie jest następujące
\(a_1 m_1=F-T_k\)

Rozpatrzmy teraz siły działające na ciało drugie. Siła tarcia występuje między dwoma ciałami, więc zgodnie z III zasadą dynamiki, na platformę działa siła \(T_k\) o zwrocie przeciwnym, powodująca jej ruch. Platforma umieszczona jest na kołach, więc możemy zaniedbać siłę tarcia pomiędzy kołami a podłożem. Drugie równanie ma więc następująca postać:
\(a_2m_2=T_k\)

Polecenie

Oblicz przyspieszenia skrzyni i platformy. Wybierz jeden zestaw prawidłowych wyników, wśród czterech przedstawionych poniżej.

Wybór 1 z 4

\(\displaystyle{a_1=4\,\mathrm{\frac{m}{s^2}}}\)
\(\displaystyle{a_2=0,2\,\mathrm{\frac{m}{s^2}}}\)

Odpowiedź nieprawidłowa

Wybór 2 z 4

\(\displaystyle{a_1=8\,\mathrm{\frac{m}{s^2}}}\)
\(\displaystyle{a_2=0,4\,\mathrm{\frac{m}{s^2}}}\)

Odpowiedź prawidłowa

Wybór 3 z 4

\(\displaystyle{a_1=1\,\mathrm{\frac{m}{s^2}}}\)
\(\displaystyle{a_2=4\,\mathrm{\frac{m}{s^2}}}\)

Odpowiedź nieprawidłowa

Wybór 4 z 4

\(\displaystyle{a_1=1,2\,\mathrm{\frac{m}{s^2}}}\)
\(\displaystyle{a_2=8\,\mathrm{\frac{m}{s^2}}}\)

Odpowiedź nieprawidłowa

Rozwiązanie

Do otrzymanych równań należy podstawić wartość \(T_k=\mu_k m_1 g\), a następnie przekształcić je:

\(\left\{\begin{matrix} a_1m_1=F-T_k \\ a_2m_2=T_k \end{matrix}\right.\)
 \[\left\{\begin{matrix} a_1m_1=F-\mu_k m_1 g\\ a_2m_2=\mu_k m_1 g \end{matrix}\right.\] \[\left\{\begin{matrix} a_1=\frac{F}{m_1}-\mu_k\,g\\ a_2=\frac{m_1}{m_2}\mu_k g \end{matrix}\right.\] \[\left\{\begin{matrix} a_1=\frac{200}{20}-0,2\cdot 10 \\ a_2=\frac{20}{100}\cdot 0,2\cdot 10 \end{matrix}\right.\] 
\(\left\{\begin{matrix} a_1=8\,\mathrm{\frac{m}{s^2}} \\ a_2=0,4\,\mathrm{\frac{m}{s^2}}  \end{matrix}\right.\)

Odpowiedź

Przyspieszenie skrzyni wynosi \(\displaystyle{a_1=8\,\mathrm{\frac{m}{s^2}}}\), natomiast platformy ma wartość \(\displaystyle{a_2=0,4\,\mathrm{\frac{m}{s^2}}}\).