Zadanie 3.4.1.6
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.4. Proste układy mechaniczne
  4. 3.4.1 Nauka
  5. Zadanie 3.4.1.6

 Zadanie 3.4.1.6

Bloczek i równia
Na powierzchni klina, nachylonej pod kątem \(30^{\circ}\) do poziomu, umieszczono klocek o masie \(m=3\,\mathrm{kg}\). Klocek ten jest połączony przy pomocy nieważkiego i nierozciągliwego sznura, poprzez nieważki bloczek, z wiszącym ciężarkiem o masie \(M=6,5\,\mathrm{kg}\) (rysunek). Zakładając brak tarcia między klockiem a powierzchnią klina, znajdź wartość przyspieszenia klocka o masie \(3\,\mathrm{kg}\).

Rysunek

 Wskazówka teoretyczna

 Teoria - zasady dynamiki
I zasada dynamiki

W inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.
Zgodnie z  I zasadą dynamiki, suma sił działających na układ musi wynosić zero.

II zasada dynamiki

Jeśli siły działające na ciało nie równoważą się, to ciało porusza się z przyspieszeniem wprost proporcjonalnym do siły wypadkowej, a odwrotnie proporcjonalnym do masy ciała. \[ \vec{a} = \frac{ \sum \vec{F}_{w} } {m} \left[ \frac{m}{s^2} = \frac{N}{kg} \right] \]
III zasada dynamiki

Jeśli ciało \(A\) działa na ciało \(B\) pewną siłą (siłą akcji), to ciało \(B\) działa na ciało \(A\) siłą (siłą reakcji) o takiej samej wartości i kierunku, lecz przeciwnym zwrocie. \[ \vec{F}_{AB} = -\vec{F}_{BA} \]

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- kąt nachylenia klina \(\alpha=30^{\circ}\),
- masa pierwszego klocka \(m=3\,\mathrm{kg}\),
- masa drugiego klocka \(M=6,5\,\mathrm{kg}\),
- przyspieszenie ziemskie \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}}}\).

Szukane:
- przyspieszenie klocka lżejszego \(a\).

Analiza sytuacji

Ponieważ sznur jest nierozciągliwy, to obydwa ciała poruszają się z tą samą wartością przyspieszenia, a ponieważ bloczek i sznur są nieważkie (zakładamy, że ich masa jest dużo mniejsza od mas obu ciał), wartości sił naprężenia sznura z obu jego końców są takie same. Oba ciała poruszają się ruchem przyspieszanym, więc zastosujemy II zasadę dynamiki do opisu ich ruchu. Aby znaleźć siłę wzajemnego oddziaływania (poprzez sznur) zastosujemy III zasadę dynamiki.

Zastosujemy II zasadę dynamiki do każdego z poruszających się ciał. W tym celu najpierw sporządzamy diagram sił działających na klocek i ciężarek. Dla każdego z ciał wprowadzamy osobny układ współrzędnych \(xy\). Siły działające na ciała i przyspieszenia ciał są reprezentowane przez ich wartości bezwzględne.

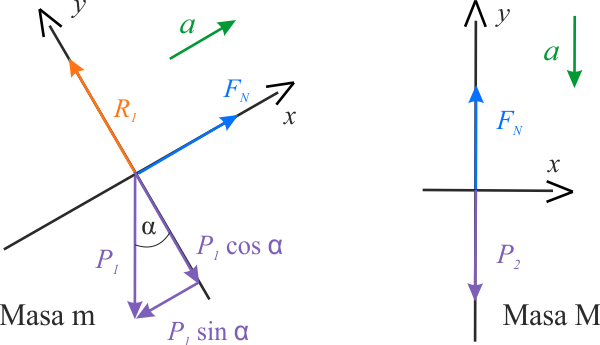
Rysunek


Diagram sił działających na klocek przedstawia rysunek po lewej, a diagram sił działających na ciężarek przedstawia rysunek po prawej stronie. W przypadku klocka wygodnie jest zastąpić, działającą na niego siłę grawitacji, równoważną sumą dwu sił: siły działającej wzdłuż powierzchni klocka i siły do niej prostopadłej. Na podstawie II zasady dynamiki możemy, dla każdego z ciał, napisać równania wiążące działające na nie siły z ich przyspieszeniem:

Dla klocka na równi
\(\eqalign{\sum F_x &=F_N-mg\sin \alpha=ma \\ \sum F_y &=R_1-mg\cos \alpha=0 }\)

Dla ciężarka
\(\sum F_y=Mg-F_N=Ma\)

Interesujące nas równanie dla kierunku \(x\), dla klocka i \(y\) dla ciężarka. Równanie dla kierunku \(y\), dla klocka, wyrażające równowagę sił w tym kierunku, byłoby potrzebne, gdyby między klockiem a klinem działała siła tarcia.

Rozwiązanie

Z analizy sytuacji otrzymaliśmy następujące równania:

\(\eqalign{ma &=F_N-mg\sin \alpha \\ Ma &=Mg-F_N }\)

Ponieważ niewiadomą jest wartość przyspieszenia \(a\), eliminujemy z pierwszego równania siły wzajemnego naprężenia sznura \(F_N\), dodając stronami oba równania. Po prostych przekształceniach otrzymujemy:

\(a(m+M)=Mg-mg\sin \alpha\)

\(\displaystyle{a=\frac{g(M-m\sin \alpha)}{m+M}}\)

\(\displaystyle{a=\frac{10(6,5-3\cdot 0,5)}{3+6,5}\approx 5,26\,\mathrm{\frac{m}{s^2}} }\)

Informacja

Poniżej znajduje się analiza zachowania dwóch ciał, z których jedno porusza się po równi pochyłej. Pierwszym etapem uruchomienia animacji jest wybranie jednego z niebieskich przycisków, umieszczonych z lewej strony równi. Następnie należy kliknąć w jedno z wybranych niebieskich kółek umieszczonych na szarym pasku poniżej równi.

Odpowiedź

Przyspieszenie klocka wynosi \(\displaystyle{a\approx 5,26\,\mathrm{\frac{m}{s^2}}} \).