Zadanie 3.4.1.5
  1. Kurs obliczeniowy z fizyki
  2. 3. Zasady dynamiki
  3. 3.4. Proste układy mechaniczne
  4. 3.4.1 Nauka
  5. Zadanie 3.4.1.5

 Zadanie 3.4.1.5

Połączone klocki
Dwa klocki o masach \(m_1\) i \(m_2\), związane nieważką i nierozciągliwą nicią, leżą na poziomej desce. Do pierwszego z nich przyłożono siłę pod kątem \(\alpha\) - patrz rysunek. Oblicz przyspieszenie klocków i siłę napinającą nić. Współczynniki tarcia kinetycznego między klockami a deską wynoszą odpowiednio \(\mu_1\) oraz \(\mu_2\).

Rysunek

 Wskazówka teoretyczna

 Teoria - zasady dynamiki
I zasada dynamiki

W inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.
Zgodnie z  I zasadą dynamiki, suma sił działających na układ musi wynosić zero.

II zasada dynamiki

Jeśli siły działające na ciało nie równoważą się, to ciało porusza się z przyspieszeniem wprost proporcjonalnym do siły wypadkowej, a odwrotnie proporcjonalnym do masy ciała. \[ \vec{a} = \frac{ \sum \vec{F}_{w} } {m} \left[ \frac{m}{s^2} = \frac{N}{kg} \right] \]
III zasada dynamiki

Jeśli ciało \(A\) działa na ciało \(B\) pewną siłą (siłą akcji), to ciało \(B\) działa na ciało \(A\) siłą (siłą reakcji) o takiej samej wartości i kierunku, lecz przeciwnym zwrocie. \[ \vec{F}_{AB} = -\vec{F}_{BA} \]

Informacja

Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.

Dane i szukane

Dane:
- masa pierwszego klocka \(m_1\),
- masa drugiego klocka \(m_2\),
- współczynnik tarcia kinetycznego dla klocka pierwszego \(\mu_1\),
- współczynnik tarcia kinetycznego dla klocka drugiego \(\mu_2\),
- kąt przyłożenia siły do klocka pierwszego \(\alpha\),
- przyspieszenie ziemskie \(g\).

Szukane:
- przyspieszenie klocków \(a\),
- siła naciągająca nić \(N\).

Analiza sytuacji

Rozwiązanie zadania należy rozpocząć od zaznaczenia i nazwania sił działających na klocki.

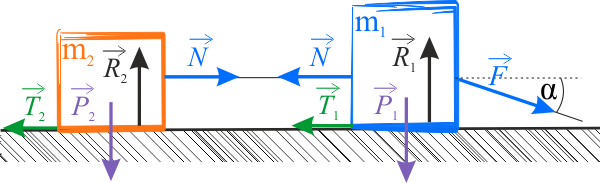
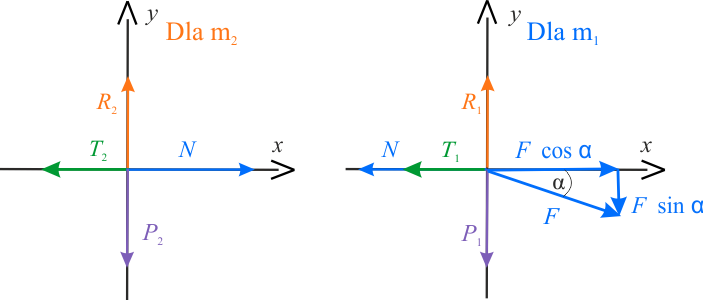
Rysunek


Na klocek pierwszy działają następujące siły:
  • siła powodująca ruch układu klocków \(\vec{F}\),
  • siła tarcia \(\vec{T_1}\),
  • siła naciągu nieważkiej nici \(\vec{N}\),
  • siła ciężkości \(\vec{P_1}\),
  • siła reakcji podłoża \(\vec{R_1}\).

Na klocek drugi działają następujące siły:
  • siła tarcia \(\vec{T_2}\),
  • siła naciągu nieważkiej nici \(\vec{N}\) - zgodnie z III zasadą dynamiki wartość tej siły jest taka sama, jak siły naciągu działającej na klocek 1,
  • siła ciężkości \(\vec{P_2}\),
  • siła reakcji podłoża \(\vec{R_2}\).

Obydwa klocki połączone są nierozciągliwą nicią i poruszają się w kierunku poziomym z tym samym przyspieszeniem \(a\). Z II zasady dynamiki Newtona wynika, że
\(\left\{\begin{matrix} m_1a= &\vec{P_1}+\vec{R_1}+\vec{F}+\vec{N}+\vec{T_1} \\ m_2a= &\vec{P_2}+\vec{R_2}+\vec{N}+\vec{T_2} \end{matrix}\right.\)

Powyżej widnieją równania zapisane w postaci wektorowej. Rozpiszmy otrzymane równania, rzutując wektory na kierunki \(x\) i \(y\).

Klocek pierwszy:
\(\left\{\begin{matrix} \sum F_x= F\cos(-\alpha)-N-T_1=m_1a \\ \sum F_y= F\sin(-\alpha)-P_1+R_1=0 \end{matrix}\right.\)

Klocek drugi:
\(\left\{\begin{matrix} \sum F_x= N-T_2=m_2a \\ \sum F_y= -P_2+R_2=0 \end{matrix}\right.\)

przedstawiające w układzie współrzędnych, siły działające na ciała.

Rysunek

Rozwiązanie

Z analizy sił, działających w rozważanym układzie klocków, uzyskaliśmy dwa układy równań. Do równań tych można napisać równania uzupełniające:

\(T_1=\mu_1R_1\),    \(T_2=\mu_2R_2\),
\(P_1=m_1g\),    \(P_2=m_2g\).

Podstawmy je do układów równań.
\(\left\{\begin{matrix} m_1a= F\cos(-\alpha)-N-\mu_1R_1 \\ 0= F\sin(-\alpha)-m_1g+R_1 \end{matrix}\right.\)     \(\left\{\begin{matrix} m_2a= N-\mu_2R_2 \\ 0= -m_2g+R_2 \end{matrix}\right.\)

Zredukujmy równania do jednego układu równań, podstawiając za \(R_1\)i \(R_2\) wartości \(R_1=m_1g-F\sin(-\alpha)\) oraz \(R_2=m_2g\):

\(\eqalign{m_1a &= F\cos(-\alpha)-N-\mu_1\left ( m_1g-F\sin(-\alpha) \right ) \\ m_2a &= N-\mu_2m_2g }\)

Otrzymane równania dodajmy stronami:

\(a(m_1+m_2)=F\cos(-\alpha)-N+N-\mu_1m_1g+\mu_1 F\sin(-\alpha)-\mu_2m_2g\)

Ponieważ funkcja sinus jest nieparzysta, a kosinus parzysta, mamy:

\(a(m_1+m_2)=F\cos(\alpha)-\mu_1m_1g-\mu_1 F\sin(\alpha)-\mu_2m_2g\)

Przyspieszenie układu klocków wynosi:

\(\displaystyle{a=\frac{F(\cos(\alpha)-\mu_1\sin(\alpha))-g\left ( \mu_1m_1+\mu_2m_2 \right ) }{m_1+m_2}}\)

Pozostało jeszcze wyznaczenie siły naciągu. W tym celu z równanie \(m_2a= N-\mu_2m_2g \) napiszemy w postaci:

\(\displaystyle{a=\frac{N-\mu_2m_2g}{m_2}}\)

Podstawiamy otrzymana wartość do równania \(m_1a= F\cos(\alpha)-N-\mu_1\left ( m_1g+F\sin(\alpha) \right )\) i otrzymujemy:

\(\displaystyle{m_1\left ( \frac{N}{m_2}-\mu_2g \right )= F\cos(\alpha)-N-\mu_1\left ( m_1g+F\sin(\alpha) \right ) }\)

Po  \[\frac{m_1}{m_2}N-\mu_2m_1g= F\cos(\alpha)-N-\mu_1m_1g-F\mu_1\sin(\alpha)\] \[\frac{m_1}{m_2}N+N= F\cos(\alpha)-\mu_1m_1g-F\mu_1\sin(\alpha) +\mu_2m_1g\] \[N\left (\frac{m_1}{m_2}+1 \right )=F \left ( \cos(\alpha)-\mu_1\sin(\alpha) \right )+m_1g(\mu_2-\mu_1)\] \[N\left (\frac{m_1+m_2}{m_2} \right )=F \left ( \cos(\alpha)-\mu_1\sin(\alpha) \right )+m_1g(\mu_2-\mu_1)\]  mamy:
\(\displaystyle{N=\frac{m_2}{m_1+m_2} \left [ F\left ( \cos(\alpha)-\mu_1\sin(\alpha) \right )+m_1g(\mu_2-\mu_1) \right ] }\)

Odpowiedź

Przyspieszenie układu klocków wynosi: \(\displaystyle{a=\frac{F(\cos(\alpha)-\mu_1\sin(\alpha))-g\left ( \mu_1m_1+\mu_2m_2 \right ) }{m_1+m_2}}\), zaś siła naciągu nici przyjmuje wartość \(\displaystyle{N=\frac{m_2}{m_1+m_2} \left [ F\left ( \cos(\alpha)-\mu_1\sin(\alpha) \right )+m_1g(\mu_2-\mu_1) \right ] }\).