Zadanie 3.4.1.4
Wskazówka teoretyczna
W inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.
Zgodnie z I zasadą dynamiki, suma sił działających na układ musi wynosić zero.
II zasada dynamiki
Jeśli siły działające na ciało nie równoważą się, to ciało porusza się z przyspieszeniem wprost proporcjonalnym do siły wypadkowej, a odwrotnie proporcjonalnym do masy ciała. \[ \vec{a} = \frac{ \sum \vec{F}_{w} } {m} \left[ \frac{m}{s^2} = \frac{N}{kg} \right] \]
III zasada dynamiki
Jeśli ciało \(A\) działa na ciało \(B\) pewną siłą (siłą akcji), to ciało \(B\) działa na ciało \(A\) siłą (siłą reakcji) o takiej samej wartości i kierunku, lecz przeciwnym zwrocie. \[ \vec{F}_{AB} = -\vec{F}_{BA} \]
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- masa ciała pierwszego \(m_1\),
- masa ciała drugiego \(m_2\),
- przyspieszenie ziemskie \(g\).
Szukane:
- przyspieszenie masy drugiej \(a_2\).
Analiza sytuacji
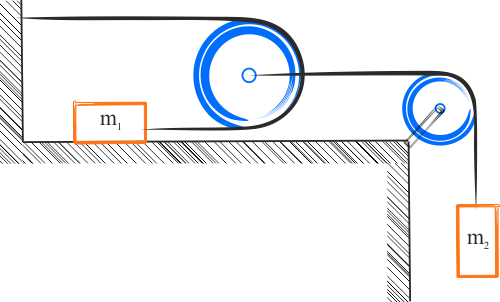
W pokazanym układzie bloczków jeden bloczek jest ruchomy i jeden nieruchomy. Bloczek mniejszy jest nieruchomy, ponieważ krążek ten może się tylko obracać, nie zaś poruszać ruchem postępowym. Bloczek większy może poruszać się równolegle do płaszczyzny, na której leży ciało o masie \(m_1\).
W pierwszym kroku można zastanowić się, jakie siły działają na ciała. Masa pierwsza zamocowana jest na innej linie niż masa druga, więc na obydwa ciała będzie działać inna siła naciągu. Na ciało pierwsze działa siła naciągu \(F_{N1}\) zaś na drugie - siła \(F_{N2}\), a ponieważ bloczki są idealnie gładkie oraz należy zaniedbać tarcie, więc wszystkie zaznaczone siły naciągu, na danej linie, są takie same.
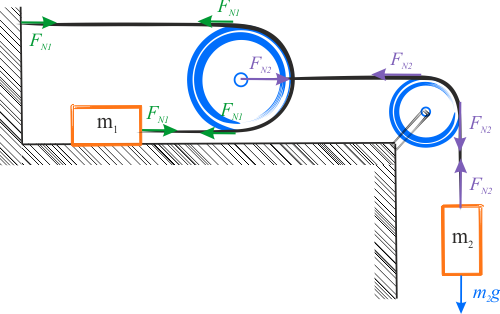
W przedstawionym układzie znajdują się dwa ciała, dla których należy napisać równania dla każdej z mas, ale najpierw trzeba się upewnić, czy przyspieszenia obu mas są takie same. Przyspieszenie nie są takie same, a między nimi zachodzi zależność Przyspieszenie masy \(m_2\) jest dwa razy mniejsze od przyspieszenia masy \(m_1\). Wynika to z tego, że masę \(m_2\) ograniczają dwie siły naciągu i podczas, gdy masa \(m_1\) przebędzie drogę \(S\) to masa \(m_2\) przebędzie drogę \(\displaystyle{\frac{1}{2}S}\). Jak wiadomo wartość przyspieszenia jest proporcjonalna do przebytej drogi: zatem \(a_1=2a_2\).
Teraz można przejść do równań opisujących siły, działające na poszczególne ciała.
Na ciało pierwsze działa siła naciągu \(F_{N1}\), stąd wynika, że
Na drugie ciało działa siła ciężkości \(m_2g\) pomniejszona o siłę naciągu \(F_{N2}\)
Otrzymaliśmy następujący układ równań
Rozwiązanie
Uzyskany układ czterech równań można uprościć do postaci
Wykonując kilka \[a_2m_2=m_2g-2\cdot 2a_2m_1\] \[a_2m_2+4a_2m_1=m_2g\] \[a_2(m_2+4m_1)=m_2g\] przekształceń otrzymujemy
Odpowiedź
Przyspieszenie masy drugiej wynosi \(\displaystyle{a_2=\frac{m_2}{m_2+4m_1}g}\).