Zadanie 3.4.1.3
Wskazówka teoretyczna
W inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.
Zgodnie z I zasadą dynamiki, suma sił działających na układ musi wynosić zero.
II zasada dynamiki
Jeśli siły działające na ciało nie równoważą się, to ciało porusza się z przyspieszeniem wprost proporcjonalnym do siły wypadkowej, a odwrotnie proporcjonalnym do masy ciała. \[ \vec{a} = \frac{ \sum \vec{F}_{w} } {m} \left[ \frac{m}{s^2} = \frac{N}{kg} \right] \]
III zasada dynamiki
Jeśli ciało \(A\) działa na ciało \(B\) pewną siłą (siłą akcji), to ciało \(B\) działa na ciało \(A\) siłą (siłą reakcji) o takiej samej wartości i kierunku, lecz przeciwnym zwrocie. \[ \vec{F}_{AB} = -\vec{F}_{BA} \]
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- masa malarza \(M=90\,\mathrm{kg}\),
- masa „krzesła bosmańskiego” \(m=15\,\mathrm{kg}\),
- czas przyspieszania malarza i krzesła \(t=1\,\mathrm{s}\),
- początkowa prędkość malarza i krzesła \(\displaystyle{v_0=0\,\mathrm{\frac{m}{s}}}\),
- końcowa prędkość malarza i krzesła \(\displaystyle{v=3\,\mathrm{\frac{m}{s}}}\),
- przyspieszenie grawitacyjne \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).
Szukane:
- siła, z jaką siłą malarz ciągnie za zwisający koniec liny \(F\),
- siła nacisku malarza na krzesło \(N\).
Analiza sytuacji
Układ ciał: malarz + „krzesło bosmańskie” porusza się w górę z jednakowym przyspieszeniem (zarówno co do kierunku, jak i co do wartości), czyli na każde ciało w układzie działa siła wypadkowa skierowana w górę. Na malarza działają siły: ciężkości \(Mg\) - w dół, siła reakcji krzesła \(R\) - w górę, równa co do wartości, zgodnie z III zasadą dynamiki, sile nacisku \(N\) malarza na krzesło oraz siła, z jaką lina działa na malarza – w górę. Ta ostatnia, zgodnie z III zasadą dynamiki, jest co do wartości równa sile, z jaką malarz ciągnie za zwisający koniec liny (siła naprężenia liny). Wypadkowa tych sił będzie powodowała ruch malarza do góry ze stałym przyspieszeniem.
Na „krzesło bosmańskie” działają siły: ciężkości \(mg\) - w dół, siła nacisku \(N\) malarza na krzesło oraz siła \(F\), z jaką drugi koniec liny działa na krzesło poprzez obudowę. Wypadkowa tych sił będzie powodowała ruch krzesła do góry ze stałym przyspieszeniem.
Ponieważ siły działające na każde ciało nie równoważą się, zastosujemy II zasadę dynamiki do rozwiązania zadania. Aby wyznaczyć przyspieszenie malarza i krzesła skorzystamy ze związku kinematycznego między prędkością a przyspieszeniem.
Opis matematyczny
Rozpatrzmy teraz siły działające niezależnie na malarza i krzesło.
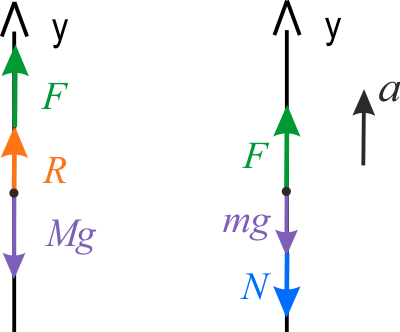
Diagramy sił, działających na ciała w jednowymiarowym układzie współrzędnych osi \(y\) skierowanej w górę, przedstawiają rysunki powyżej. Siły działające na obydwa ciała są reprezentowane przez ich wartości bezwzględne. Na podstawie diagramów sił możemy napisać równania II zasady dynamiki dla każdego z ciał:
Dla malarza
Dla „krzesła bosmańskiego”
Dodatkowo korzystając z tego, że \(R=N\) i podstawiając tę równość do pierwszego równania, otrzymujemy układ dwóch równań z dwiema niewiadomymi \(F\) i \(N\):
Wyznaczmy teraz wartość przyspieszenia \(a\), z jakim poruszał się malarz wraz z krzesłem. W tym celu skorzystamy z zależności pomiędzy prędkością a przyspieszeniem w ruchu jednostajnie przyspieszonym:
Rozwiązanie
Wartość przyspieszania, z jakim poruszał się malarz wraz z krzesłem, wynosi
Siłę, z jaką malarz ciągnie za zwisający koniec liny, obliczamy, dodając stronami równania z wyprowadzonego wcześniej układu równań.
\[2F+N-N-Mg-mg=Ma+ma\] \[2F-g(M+m)=Ma+ma\] \[2F=a(M+m)+g(M+m)\]
Siłę nacisku malarza na krzesło obliczamy odejmując stronami równania z wyprowadzonego wcześniej układu równań.
\[F-F+N+N-Mg+mg=Ma-ma\] \[2N-g(M-m)=a(M-m)\] \[2N=a(M-m)+g(M-m)\] \[2N=(M-m)(a+g)\]
Odpowiedź
Siła nacisku malarza na krzesło wynosi \(\displaystyle{F=682,5\,\mathrm{N}}\), wartość siły, z jaką malarz ciągnie za zwisający koniec liny jest następująca \(\displaystyle{F=487,5\,\mathrm{N}}\).

