Zadanie 3.4.1.2
Na linie, przerzuconej przez nieruchomy blok i przyczepionej do ciężarka o masie \(75\,\mathrm{kg}\), znajduje się człowiek o masie \(70\,\mathrm{kg}\). Przyjmij, że lina jest nieważka i nierozciągliwa oraz ślizga się po bloku bez tarcia. Wyznacz, z jakim przyspieszeniem względem Ziemi, będzie poruszać się ciężarek w następujących przypadkach:
a) człowiek wspina się po linie ze stałą prędkością \(\displaystyle{2\frac{m}{s}}\) względem liny,
b) człowiek wspina się po linie ze stałym przyspieszeniem \(\displaystyle{0,5\frac{m}{s^2}}\) względem liny.
Do obliczeń przyjmij, że przyspieszenie grawitacyjne wynosi \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\).
Wskazówka teoretyczna
W inercjalnym układzie odniesienia, jeśli na ciało nie działa żadna siła lub siły działające równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.
Zgodnie z I zasadą dynamiki, suma sił działających na układ musi wynosić zero.
II zasada dynamiki
Jeśli siły działające na ciało nie równoważą się, to ciało porusza się z przyspieszeniem wprost proporcjonalnym do siły wypadkowej, a odwrotnie proporcjonalnym do masy ciała. \[ \vec{a} = \frac{ \sum \vec{F}_{w} } {m} \left[ \frac{m}{s^2} = \frac{N}{kg} \right] \]
III zasada dynamiki
Jeśli ciało \(A\) działa na ciało \(B\) pewną siłą (siłą akcji), to ciało \(B\) działa na ciało \(A\) siłą (siłą reakcji) o takiej samej wartości i kierunku, lecz przeciwnym zwrocie. \[ \vec{F}_{AB} = -\vec{F}_{BA} \]
Informacja
Postaraj się samodzielnie rozwiązać zadanie. Możesz sprawdzić swój tok rozumowania, klikając w przyciski odsłaniające kolejne etapy proponowanego rozwiązania lub sprawdź od razu odpowiedź.
Dane i szukane
Dane:
- masa ciężarka \(M=75\,\mathrm{kg}\),
- masa człowieka \(m=70\,\mathrm{kg}\),
- przyspieszenie grawitacyjne \(\displaystyle{g=10\,\mathrm{\frac{m}{s^2}} }\),
- prędkość człowieka względem liny \(v=\displaystyle{2\frac{m}{s}}\) - punkt a),
- przyspieszenie człowieka względem liny \(a_c=\displaystyle{0,5\frac{m}{s^2}}\) - punkt b).
Szukane:
- przyspieszenie ciężarka względem Ziemi \(a\).
Analiza sytuacji
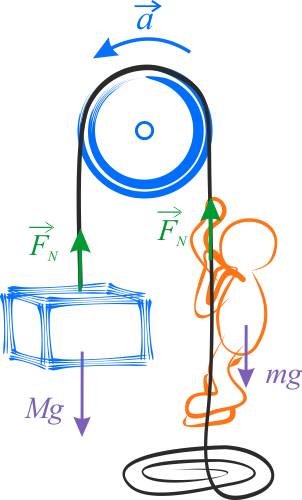
Ponieważ lina jest nierozciągliwa, człowiek i blok poruszają się z jednakową prędkością i jednakowym przyspieszeniem względem Ziemi (bloczka). Zarówno człowiek jak i ciężarek poruszają się pod wpływem następujących sił: siły ciężkości w dół oraz siła naprężenia liny w górę. Ponieważ lina jest nieważka i ślizga się po bloku bez tarcia, to wartości sił naprężenia obu końców sznura są takie same. Wnioskujemy, że ponieważ ciężarek ma większą masę niż człowiek to, gdyby człowiek względem liny był w spoczynku, człowiek poruszałby się w górę a ciężarek w dół. W takiej sytuacji siła naprężenia sznura jest mniejsza od siły ciężkości ciężarka i większa od siły ciężkości człowieka. Jeżeli człowiek wspina się po linie ze stałą prędkością względem liny, to jego przyspieszenie względem Ziemi nie ulega zmianie, czyli jest takie samo jak wtedy, gdy człowiek względem Ziemi jest w spoczynku. Jeżeli człowiek wspina się po linie ze stałym przyspieszeniem względem liny, to jego przyspieszenie względem Ziemi różni się od przyspieszenia ciężarka o tę właśnie wartość.
1. – bloczek obraca się wraz z nicią oraz
2. – nić ślizga się po bloczku.
Z treści zadania wynika, że chodzi o przypadek 1., gdyż stwierdzenie, iż bloczek jest nieważki, oznacza, podobnie jak dla nici, zaniedbanie jego masy, a to ma znaczenie, gdy bloczek się obraca. Uwzględnienie masy bloczka prowadziłoby nas do zagadnienia z dynamiki ruchu obrotowego bryły sztywnej. W przypadku 2. – nici ślizgającej się po bloczku warunkiem aby wartości sił naprężenia obu końców nici były takie same, jest to, że między nicią a bloczkiem nie ma tarcia.
Rozwiązanie - przypadek a)
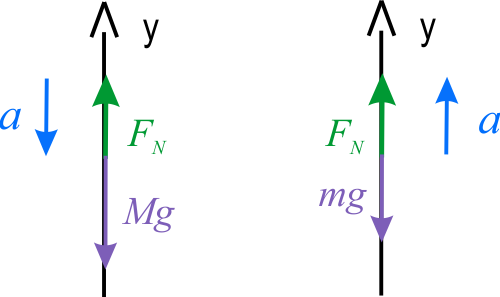
Na rysunku przedstawiono diagramy sił działających na oba ciała w układzie współrzędnych osi \(OY\) skierowanej w górę. Na diagramach siły są reprezentowane przez ich wartości bezwzględne. Masa ciężarka jest większa niż masa człowieka, dlatego, rozsądnym będzie przyjęcie, że ciężarek porusza się z w dół z pewnym przyspieszeniem. Jeżeli nasze założenie jest słuszne to w rozwiązaniu otrzymamy wartość dodatnią przyspieszenia, w przeciwnym przypadku wyjdzie nam wartość ujemna oznaczająca, że przyspieszenie ciężarka ma przeciwny kierunek do przyjętego na początku. Ponieważ prędkość człowieka względem liny jest stała, to wartości przyspieszeń obu ciał są takie same i z II zasady dynamiki, dla obu ciał otrzymujemy:
1. Dla bloczka mamy
2. Dla człowieka mamy
Ponieważ nie interesuje nas naprężenie sznura, więc eliminujemy \(F_N\) przez odjęcie stronami obu równań, otrzymując jedno równanie na \(a\), którego rozwiązaniem jest
\[F_N-F_N-Mg+mg=-Ma-ma\] \[-g(M-m)=-a(M+m)\]
Rozwiązanie - przypadek b)
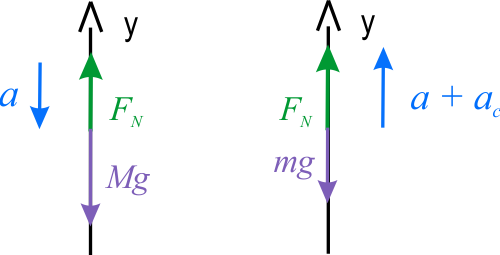
Na rysunku przedstawiono diagramy sił działających na oba ciała w układzie współrzędnych osi \(OY\) skierowanej w górę. Na diagramach siły są reprezentowane one przez ich wartości bezwzględne. Równanie II zasady dynamiki zapisane dla bloczka, podobnie jak w punkcie a) ma postać
Ponieważ człowiek wspina się po linie z przyspieszeniem \(a_c\) względem liny, to jego przyspieszenie względem Ziemi będzie sumą przyspieszeń liny względem Ziemi i jego przyspieszenia względem liny. II zasada dynamiki zapisana dla człowieka, ma postać
Po odjęciu stronami obu równań i eliminacji naprężenia sznura \(F_N\) otrzymujemy jedno równanie na \(a\), którego rozwiązaniem jest
\[F_N-F_N-Mg+mg=-Ma-m(a+a_c)\] \[-g(M-m)=-Ma-ma-ma_c)\] \[g(M-m)-ma_c=a(M+m)\]
Odpowiedź
W pierwszym przypadku ciężarek będzie poruszał się z przyspieszeniem \(\displaystyle{a\approx0,345\frac{m}{s^2} }\), w drugim przypadku otrzymujemy wynik \(\displaystyle{a\approx0,103\frac{m}{s^2} }\).